Question

【题目】已知∠ABC=90°，点P为射线BC上任意一点（点P与点B不重合），分别以AB、AP为边在∠ABC的内部作等边△ABE和△APQ，连接QE并延长交BP于点F．

（1）如图1，若AB=，点A，E，P恰好在一条直线上时，求EF的长（直接写出结果）；

（2）如图2，当点P为射线BC上任意一点时，求证：BF=EF；

（3）若AB=，设BP=2，求QF的长．

Answer 1

【答案】（1）1；（2）见解析；（3）3.

【解析】

（1）根据A、E、P在同一直线上判断出点E是AP的中点，先根据直角三角形30°角所对的直角边等于斜边的一半求出AP，然后根据等边三角形的性质求出QE．再根据直角三角形的性质求出QF，然后根据EF=QF﹣QE，代入数据进行计算即可；（2）先求出∠BAP=∠EAQ，然后利用“边角边”证明△ABP≌△AEQ，根据全等三角形对应角相等可得∠AEQ=∠ABP=90°，然后求出∠BEF=∠EBF=30°，再根据等角对等边的性质即可得证；（3）过点F作FD⊥BE于点D，根据等腰三角形三线合一的求出BD，再解直角三角形求出BF的长度，即可得到EF的长，再根据全等三角形对应边相等可得QE=BP，然后代入数据进行计算即可．

解：（1）∵△ABE是等边三角形，A、E、P在同一直线上，

∴AB=AE，∠BAE=60°，

∴∠APB=30°，

∴AP=2AB=2，

∴点E是AP的中点，

∴QE⊥AP，

∴QE=3，

∵∠APQ=60°，∠APB=30°，

∴∠QPF=90°，

∴QF=4，

∴EF=QF﹣QE=1；

（2）证明：∵∠BAP=∠BAE﹣∠EAP=60°﹣∠EAP，

∠EAQ=∠QAP﹣∠EAP=60°﹣∠EAP，

∴∠BAP=∠EAQ．

在△ABP和△AEQ中，

，

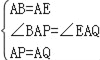∴△ABP≌△AEQ（SAS），

∴∠AEQ=∠ABP=90°，

∴∠BEF=180°﹣∠AEQ﹣∠AEB=180°﹣90°﹣60°=30°，

∵∠EBF=90°﹣60°=30°，

∴∠BEF=∠EBF，

∴EF=BF；

（3）如图，过点F作FD⊥BE于点D，

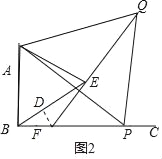
∵△ABE是等边三角形，

∴BE=AB=，

由（2）得∠EBF=30°，

在Rt△BDF中，BD=BE=，

∴BF==1，

∴EF=1，

∵△ABP≌△AEQ，

∴QE=BP=2，

∴QF=QE+EF=2+1=3．