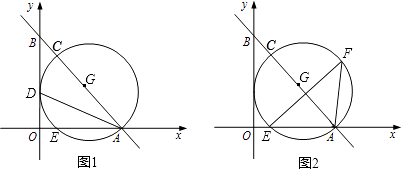题目内容
【题目】定义:有两条边长的比值为 ![]() 的直角三角形叫“潜力三角形”.如图,在△ABC中,∠B=90°,D是AB的中点,E是CD的中点,DF∥AE交BC于点F.
的直角三角形叫“潜力三角形”.如图,在△ABC中,∠B=90°,D是AB的中点,E是CD的中点,DF∥AE交BC于点F.
(1)设“潜力三角形”较短直角边长为a,斜边长为c,请你直接写出 ![]() 的值为;
的值为;
(2)若∠AED=∠DCB,求证:△BDF是“潜力三角形”;
(3)若△BDF是“潜力三角形”,且BF=1,求线段AC的长.
【答案】
(1)2或 ![]()
(2)
解:证明:延长AE交BC于G,如图所示:

∵DF∥AE,D是AB的中点,
∴∠AED=∠CDF,BF=GF,
∵∠AED=∠DCB,
∴∠CDF=∠DCB,
∴DF=CF,
∵DF∥AE,E是CD的中点,
∴CG=GF,
∴BF=GF=CG,
∴DF=CF=2GF=2BF,
∴ ![]() =
= ![]() ,
,
又∵∠B=90°,
∴△BDF是“潜力三角形”;
(3)
解:分四种情况:
①当 ![]() =
= ![]() 时,
时,
∵BF=1,
∴GF=CG=BF=1,BD=2,
∴AB=2BD=4,BC=3,
∴AC= ![]() =
= ![]() =5;
=5;
②当 ![]() =
= ![]() 时,DF=2BF=2,
时,DF=2BF=2,
∴BD= ![]() =
= ![]() =
= ![]() ,
,
∴AB=2BD=2 ![]() ,
,
∵BC=3,∠B=90°,
∴AC= ![]() =
= ![]() =
= ![]() ;
;
③当 ![]() =
= ![]() 时,BD=
时,BD= ![]() BF=
BF= ![]() ,
,
∴AB=2BD=1,
∵BC=3,∠B=90°,
∴AC= ![]() =
= ![]() =
= ![]() ;
;
④当 ![]() =
= ![]() 时,
时,
设BD=x,则DF=2x,
由勾股定理得:(2x)2﹣x2=12,
解得:x= ![]() ,
,
∴AB=2BD= ![]() ,
,
∵BC=3,∠B=90°,
∴AC= ![]() =
= ![]() =
= ![]() ;
;
综上所述:若△BDF是“潜力三角形”,且BF=1,线段AC的长为5或 ![]() 或
或 ![]() 或
或 ![]() .
.
【解析】(1)解:分两种情况:
①当 ![]() =
= ![]() 时,
时, ![]() =2;
=2;
②设另一条直角边长为b,当 ![]() =
= ![]() 时,b=2a,
时,b=2a,
∵∠B=90°,
∴c= ![]() =
= ![]() a,
a,
∴ ![]() =
= ![]() ;
;
所以答案是:2或 ![]() ;
;
【考点精析】通过灵活运用三角形的“三线”,掌握1、三角形角平分线的三条角平分线交于一点(交点在三角形内部,是三角形内切圆的圆心,称为内心);2、三角形中线的三条中线线交于一点(交点在三角形内部,是三角形的几何中心,称为中心);3、三角形的高线是顶点到对边的距离;注意:三角形的中线和角平分线都在三角形内即可以解答此题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某面粉加工厂加工的面粉,用每袋可装10g面粉的袋子装了200袋经过称重,质量超过标准质量10kg的用正数表示,质量低于标准质量10kg的用负数表示,结果记录如下
与标准质量的偏差(kg) | ﹣1.5 | ﹣1 | ﹣0.5 | 0 | 0.5 | 1 | 2 |
袋数(袋) | 40 | 30 | 10 | 25 | 40 | 20 | 35 |
(1)求这批面粉的总质量;
(2)如果100kg小麦加工80kg面粉,那么这批面粉是由多少千克小麦加工的?