Question

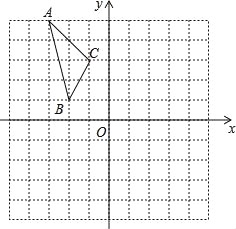
【题目】已知，如图，△ABC 中，D 是 BC 的中点，AB＝5，AC＝3，AD＝2．

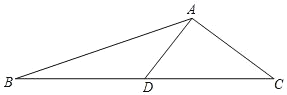
（1）按要求画图：延长 AD 至点 E，使 DE＝AD，连接 BE；

（2）求 BC 的长度．

Answer 1

【答案】（1）见解析；（2）

【解析】

（1）根据几何语言画出对应的图形即可；

（2）先证明△BDE≌△CDA，得到BE＝AC＝3，再利用勾股定理的逆定理证明△ABE为直角三角形，∠AEB＝90°，然后根据勾股定理计算出BD，从而得到BC的长．

解：（1）如图所示；

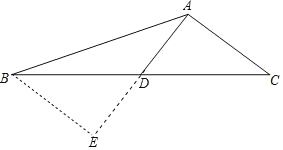
（2）∵D 是 BC 的中点，

∴BD＝CD，

在△BDE 和△CDA 中，，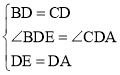

∴△BDE≌△CDA，

∴BE＝AC＝3，

∵AE＝2AD＝4，AB＝5，

∴AE2＋BE2＝AB2，

∴△ABE 为直角三角形，∠AEB＝90°，

在Rt△BDE中，BD＝，

∴BC＝2BD＝．