题目内容
【题目】如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点A(x1,0)、B(x2,0),我们把|x1﹣x2|记为d(A、B),抛物线的顶点到x轴的距离记为d(x),如果d(A,B)=d(x),那么把这样的抛物线叫做“正抛物线”.
(1)抛物线y=2x2﹣2是不是“正抛物线”;(回答“是”或“不是”).
(2)若抛物线y=﹣x2+bx(b>0)是“正抛物线”,求抛物线的解析式;
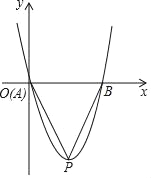
(3)如图,若“正抛物线”y=x2+mx(m<0)与x轴相交于A、B两点,点P是抛物线的顶点,则抛物线上是否存在点C,使得△PAC是以PA为直角边的直角三角形?如果存在,请求出C的坐标;若不存在,请说明理由.
【答案】(1)抛物线y=2x2﹣2是“正抛物线”;(2)抛物线的解析式为y=﹣x2+4x;(3)满足条件的点C坐标为(![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() ).
).
【解析】
(1)根据“正抛物线”的定义判断即可;
(2)根据“正抛物线”的定义构建方程即可解决问题;
(3)首先求出m,分两种情形分别求解即可解决问题;
(1)对于抛物线y=2x2﹣2,
当y=0时,2x2﹣2=0,解得x=1或﹣1,
∴A(﹣1,0),B(1,0),
∴d(A,B)=2,
![]()
∴d(x)=d(A,B),
∴抛物线y=2x2﹣2是“正抛物线”.
故答案为:是.
(2)当y=0时,﹣x2+bx=0,解得x=0或b,
∵b>0,
∴d(A,B)=b,
由题意![]()
解得b=0(舍弃)或b=4,
∴抛物线的解析式为![]()
(3)当y=0时,x2+mx=0,解得x=0或﹣m,
∵m<0,
∴d(A,B)![]()
∵![]()
∴d(x)![]()
由题意![]()
解得![]() 或0(舍弃),
或0(舍弃),
∴![]()
假设存在点C,使得△PAC是以PA为直角边的直角三角形,分两种情形:
①如图1中,作AC⊥AP交抛物线于点C,厉害PC,作PE⊥x轴交AC于D.
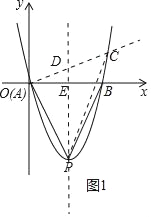
![]()
∴AE=2,PE=4,
由△ADE∽△PAE,可得![]()
∴![]()
∴DE=1,
∴D(2,1),
∴直线AD的解析式为![]()
由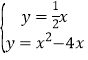 解得
解得![]() 或
或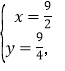
∴![]()
②如图2中,作PC⊥AP交抛物线于C,交y轴于D,连接AC,作PE⊥x轴于E.
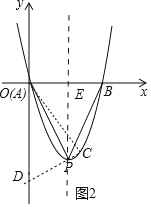
由△ADP∽△PAE,可得![]() 即
即![]()
∴![]()
∴AD=5,
∴D(0,5),
∴直线AD的解析式为![]()
由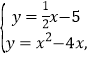 解得
解得![]() 或
或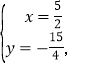
综上所述,满足条件的点C坐标为(92,94)或(52,154).
综上所述,满足条件的点C坐标为![]() 或
或![]()