Question

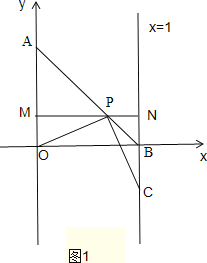
【题目】如图，以O为原点的直角坐标系中，A点的坐标为（0，1），直线x=1交x轴于点B．点为线段AB上一动点，作直线PC⊥PO，交直线x=1于点C．过P点作直线MN平行于x轴，交y轴于点M，交直线x=1于点N．记AP=x，△PBC的面积为S．

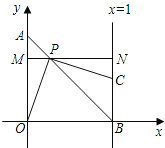
（1）当点C在第一象限时，求证：△OPM≌△PCN；

（2）当点P在线段AB上移动时，点C也随之在直线x=1上移动，求出S与x之间的函数关系式，并写出自变量的取值范围；

（3）当点P在线段AB上移动时，△PBC是否可能成为等腰三角形？如果可能，直接写出所有能使△PBC成为等腰三角形的x的值；如果不可能，请说明理由．

Answer 1

【答案】（1）见解析；（2）S=x2﹣x+（＜x＜）．（3）点P的坐标为（0，1）或（，1﹣）．

【解析】

试题分析：（1）根据∠OPC=90°和同角的余角相等，我们可得出△OPM和△PCN中两组对应角相等，要证两三角形全等，必须有相等的边参与，已知了OA=OB，因此三角形OAB是等腰直角三角形，那么△AMP也是个等腰三角形，AM=MP，OA=OB=MN，由此我们可得出OM=PN，由此我们可得出两三角形全等．

（2）分两种情况进行讨论：①点C在第一象限时，②点C在第四象限时．分别利用S=S△PBC=BCPN求解即可．

（3）要分两种情况进行讨论：①当C在第一象限时，要想使PCB为等腰三角形，那么PC=CB，∠PBC=45°，因此此时P与A重合，那么P的坐标就是A的坐标．②当C在第四象限时，要想使PCB为等腰三角形，那么PB=BC，在等腰RT△PBN中，我们可以用x表示出BP的长，也就表示出了BC的长，然后根据（1）中的全等三角形，可得出MP=NC，那么可用这两个含未知数x的式子得出关于x的方程来求出x的值．那么也就求出了PM、OM的长，也就得出了P点的坐标．

证明：（1）如图，

∵OM∥BN，MN∥OB，∠AOB=90°

∴四边形OBNM为矩形

∴MN=OB=1，∠PMO=∠CNP=90°

∵OA=OB，

∴∠1=∠3=45°

∵MN∥OB

∴∠2=∠3=45°

∴∠1=∠2=45°，

∴AM=PM

∴OM=OA﹣AM=1﹣AM，PN=MN﹣PM=1﹣PM

∴OM=PN

∵∠OPC=90°，

∴∠4+∠5=90°，

又∵∠4+∠6=90°，

∴∠5=∠6

∴△OPM≌△PCN

（2）解：①点C在第一象限时，

∵AM=PM=APsin45°=x

∴OM=PN=1﹣x，

∵△OPM≌△PCN

∴CN=PM=x，

∴BC=OM﹣CN=1﹣x﹣x=1﹣x，

∴S=S△PBC=BCPN=×（1﹣x）（1﹣x）=x2﹣x+（0≤x＜）．

②如图1，点C在第四象限时，

∵AM=PM=APsin45°=x

∴OM=PN=1﹣x，

∵△OPM≌△PCN

∴CN=PM=x，

∴BC=CN﹣OM=x﹣（1﹣x）=x﹣1，

∴S=S△PBC=BCPN=×（1﹣x）（x﹣1）=x2﹣x+（＜x＜）．

（3）解：△PBC可能成为等腰三角形

①当P与A重合时，PC=BC=1，此时P（0，1）

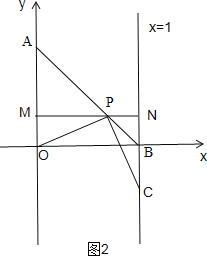
②如图，当点C在第四象限，且PB=CB时

有BN=PN=1﹣x

∴BC=PB=PN=﹣x

∴NC=BN+BC=1﹣x+﹣x

由（2）知：NC=PM=x

∴1﹣x+﹣x=x

整理得（+1）x=+1

∴x=1

∴PM=x=，BN=1﹣x=1﹣，

∴P（，1﹣）

由题意可知PC=PB不成立

∴使△PBC为等腰三角形的点P的坐标为（0，1）或（，1﹣）．