题目内容
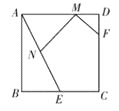
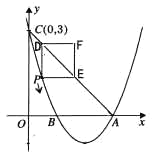
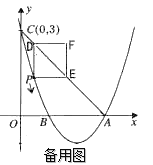
【题目】如图,在平面直角坐标系中,矩形ABCD的顶点A、B、C的坐标分别为(0,5)(0,2)(4,2),直线l的解析式为y = kx+5-4k(k > 0).
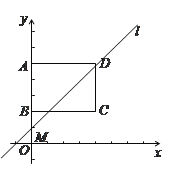
(1)当直线l经过点B时,求一次函数的解析式;
(2)通过计算说明:不论k为何值,直线l总经过点D;
(3)直线l与y轴交于点M,点N是线段DM上的一点, 且△NBD为等腰三角形,试探究:
①当函数y = kx+5-4k为正比例函数时,点N的个数有 个;
②点M在不同位置时,k的取值会相应变化,点N的个数情况可能会改变,请直接写出点N所有不同的个数情况以及相应的k的取值范围.
【答案】(1)y =![]() x+2;(2)说明见解析;(3)①2;②;当k≥2时,有3个点;当
x+2;(2)说明见解析;(3)①2;②;当k≥2时,有3个点;当![]() <k<2时,有2个点;当k=
<k<2时,有2个点;当k=![]() 时,有0个;当0<k<
时,有0个;当0<k<![]() 时,有1个.
时,有1个.
【解析】
(1)将点B坐标代入解析式求出k的值;
(2)将点D的坐标代入解析式,得出答案;
(3)根据图形的平行法则求出零界值,然后进行分类.
解: (1)将点B(0,2)代入y=kx+5-4k得![]()
∴y =![]() x+2
x+2
(2)由题意可得:点D坐标为(4,5)
把x=4代入y=kx+5-4k得y=5 ∴不论k为何值,直线l总经点D;
(3)①当函数y=kx+5-4k为正比例函数时可得5-4k=0,解得k=![]() ,
,
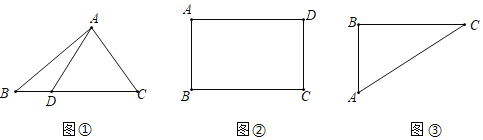
∴直线解析式为y=![]() x,则BM=2,如图1所示,
x,则BM=2,如图1所示,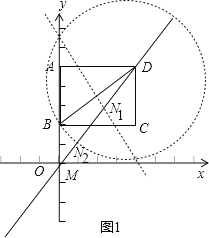
以D为圆心BD为半径画圆,与DM有一交点,BD的垂直平分线与DM有一交点,
故满足条件的点有两个.
故答案为:2;
②∵k>0,
∴5-4k<5,
当5-4k=-3时,k=2,此时OM=3,则MB=5,如图2所示,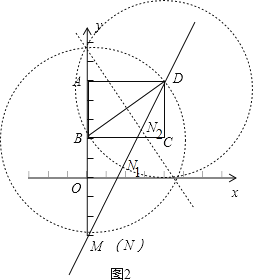
分别以B、D为圆心BD为半径画圆,与DM交于点M和N1,和BD的垂直平分线交DM于点N2,故此时满足条件的N点有3个,
当k>2时,此时MB>5,如图3所示,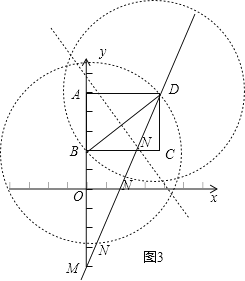
分别以B、D为圆心BD为半径画圆,与DM交于N1、N2两点,BD的垂直平分线交DM于N3,
故满足条件的点有3个,
∴当k≥2时,满足条件的点有3个,
当![]() <k<2时,此时0<OB<5,同理可得出满足条件点有两个,
<k<2时,此时0<OB<5,同理可得出满足条件点有两个,
当k=![]() 时,此时B、M重合,则满足条件的N点有0个,
时,此时B、M重合,则满足条件的N点有0个,
当0<k<![]() 时,即M在线段AB上时,同理可知满足条件的点只有一个,
时,即M在线段AB上时,同理可知满足条件的点只有一个,
综上可知当k≥2时,有3个;当![]() <k<2时,有两个;当k=
<k<2时,有两个;当k=![]() 时,有0个;当0<k<
时,有0个;当0<k<![]() 时,有1个.
时,有1个.

 作业辅导系列答案
作业辅导系列答案