Question

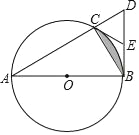
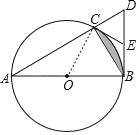
【题目】如图，已知△ABC内接于⊙O，A B为⊙O的直径，BD⊥AB，交AC的延长线于点D．

（1）E为BD的中点，连结CE，求证：CE是⊙O的切线．

（2）若AC=3，CD=1，求图中阴影部分的面积．

Answer 1

【答案】（1）详见解析；（2） ．

【解析】

连接OC，利用思路：连半径，通过角的变换，证明出CO与CE的垂直关系，即可得出结论.

证明出△OBC为等边三角形，再利用分割图形求面积法即可得出阴影部分的面积，即可得出结论.

（1）如图：连接CO，

∵A B为⊙O的直径，∴∠ACB=90°，

在Rt△BCD中，E是BD的中点，

∴∠ECB=∠EBC，

∵BD⊥AB，∴∠EBC+CBA=90°，

而∠OCB=∠CBO，

∴∠OCE=90°，

∴CE是⊙O的切线．

（2）∵∠ACB=∠BCD=90°，

∠CAB=∠CBD，∴△ACB∽△BCD，

∴BC2=ACCD，即：BC=，

AB2=BC2+AC2=3+9=12，

∴OB=AB==BC，

∴△OBC为等边三角形，

∠BOC=60°，

S阴影=S扇形BCO﹣S△BOC=﹣××=﹣．