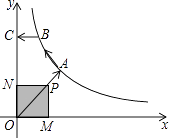
题目内容
【题目】若a＝2016×2018－2016×2017， b＝2015×2016－2013×2017，
，则a，b，c的大小关系是( )
A. a＜b＜c B. a＜c＜b C. b＜a＜c D. b＜c＜a
【答案】B
【解析】分析：根据平方差公式，对a、b变形，然后和c比较即可判断三者之间的大小.
详解：由题意可知
a＝2016×2018－2016×2017
=2016×(2018-2017)
=2016
b＝2015×2016－2013×2017
=2015×2016－(2015-2)×(2015+2)
=2015×2016－(2015-2)
=2015×2016－2015+4
=2015×(2016-2015)+4
=2015+4
=2019
∵2017=(2016+1)=2016+2×2016+1＞2016+10
∴2016＜2016+10＜2017
即2016＜
＜2017
∴a＜c＜b
故选：B.
名校课堂系列答案
【题目】大学生小张利用暑假50天在一超市勤工俭学，被安排销售一款成本为40元/件的新型商品，此类新型商品在第x天的销售量p件与销售的天数x的关系如下表：
x（天） | 1 | 2 | 3 | … | 50 |
p（件） | 118 | 116 | 114 | … | 20 |
销售单价q（元/件）与x满足：当1≤x＜25时q=x+60；当25≤x≤50时q=40+ 
．
（1）请分析表格中销售量p与x的关系，求出销售量p与x的函数关系．
（2）求该超市销售该新商品第x天获得的利润y元关于x的函数关系式．
（3）这50天中，该超市第几天获得利润最大？最大利润为多少？
【题目】二次函数y=ax2+bx+c（a，b，c为常数，且a≠0）中的x与y的部分对应值如下表：
X | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论：
（1）ac＜0；
（2）当x＞1时，y的值随x值的增大而减小．
（3）3是方程ax2+（b﹣1）x+c=0的一个根；
（4）当﹣1＜x＜3时，ax2+（b﹣1）x+c＞0．
其中正确的个数为（ ）
A.4个
B.3个
C.2个
D.1个