Question

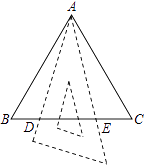
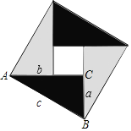
【题目】现用4个全等的直角三角形拼成如图所示“弦图”．Rt△ABC中，∠ACB=90°，若AC=b，BC=a，请你利用这个图形解决下列问题：

（1）试说明a2+b2=c2；

（2）如果大正方形的面积是6,小正方形的面积是2,求（a+b）2的值．

Answer 1

【答案】（1）详见解析；（2）10.

【解析】

（1）根据题意，我们可在图中找等量关系，由中间的小正方形的面积等于大正方形的面积减去四个直角三角形的面积，列出等式化简即可得出勾股定理的表达式．
（2）根据完全平方公式的变形解答即可．

（1）∵大正方形面积为c2，直角三角形面积为ab，小正方形面积为（b-a）2，

∴c2=4×ab+（a-b）2=2ab+a2-2ab+b2即c2=a2+b2．；

（2）由图可知，（b-a）2=2，4×ab=6-2=4，∴ab=2，

∴（a+b）2=（b-a）2+4ab=2+8=10．