题目内容
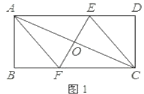
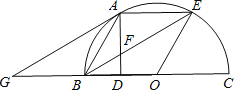
【题目】如图,点A,E是半圆周上的三等分点,直径BC=2,AD⊥BC,垂足为D,连接BE交AD于F,过A作AG∥BE交BC于G.
(1)判断直线AG与⊙O的位置关系,并说明理由.
(2)求线段AF的长.
【答案】(1)AG与⊙O相切,理由见解析(2)![]()
【解析】解:(1)直线AG与⊙O的位置关系是AG与⊙O相切,理由如下:
连接OA,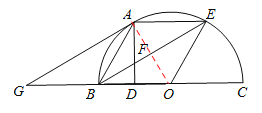
∵点A,E是半圆周上的三等分点,
∴![]() 。∴点A是
。∴点A是![]() 的中点。
的中点。
∴OA⊥BE。
又∵AG∥BE,∴OA⊥AG。∴AG与⊙O相切。
(2)∵点A,E是半圆周上的三等分点,∴∠AOB=∠AOE=∠EOC=60°。
又∵OA=OB,∴△ABO为正三角形。
又∵AD⊥OB,OB=1,∴BD=OD=![]() ,AD=
,AD=![]() 。
。
又∵∠EBC=![]() ∠EOC=30°,
∠EOC=30°,
在Rt△FBD中,FD=BDtan∠EBC=BDtan30°=![]() 。
。
∴AF=AD﹣DF=![]() 。
。
答:AF的长是![]() 。
。
(1)求出弧AB=弧AE=弧EC,推出OA⊥BE,根据AG∥BE,推出OA⊥AG,根据切线的判定即可得出答案。
(2)求出等边三角形AOB,求出BD、AD长,求出∠EBC=30°,在△FBD中,通过解直角三角形求出DF即可。

练习册系列答案
相关题目
【题目】某校为选拔一名选手参加“美丽江门,我为侨乡做代言”主题演讲比赛,经研究,按下图所示的项目和权数对选拔赛参赛选手进行考评(因排版原因统计图不完整),下表是李明、张华在选拔赛中的得分情况:

服装 | 普通话 | 主题 | 演讲技巧 | |
李明 | 85 | 70 | 80 | 85 |
张华 | 90 | 75 | 75 | 80 |
结合以上信息,回答下列问题:
(1)求服装项目在选手考评中的权数;
(2)根据你所学的知识,帮助学校在李明、张华两人中选择一人参加“美丽江门,我为侨乡做代言”主题演讲比赛,并说明理由.