جâؤ؟ؤعبف
،¾جâؤ؟،؟زرضھ£¬¾طذخ![]() ضذ£¬
ضذ£¬![]() £¬
£¬![]() µؤ´¹ض±ئ½·ض
µؤ´¹ض±ئ½·ض![]() دك·ض±ً½»
دك·ض±ً½»![]() سعµم
سعµم![]() £¬´¹×مخھ
£¬´¹×مخھ![]() £®
£®
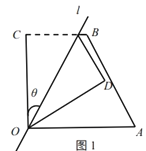
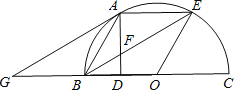
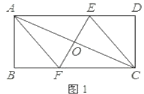
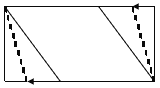
£¨1£©بçح¼1£¬ء¬½س![]() £¬اَض¤£؛ثؤ±كذخ
£¬اَض¤£؛ثؤ±كذخ![]() خھءâذخ£»
خھءâذخ£»
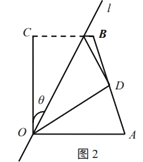
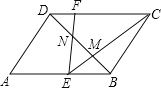
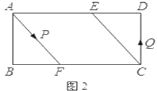
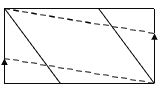
£¨2£©بçح¼2£¬¶¯µم![]() ·ض±ً´س
·ض±ً´س![]() ء½µمح¬ت±³ِ·¢£¬رط
ء½µمح¬ت±³ِ·¢£¬رط![]() ؛ح
؛ح![]() ¸÷±كشبثظشث¶¯ز»ضـ£¬¼´µم
¸÷±كشبثظشث¶¯ز»ضـ£¬¼´µم![]() ×ش
×ش![]() ح£ض¹£¬µم
ح£ض¹£¬µم![]() ×ش
×ش![]() ح£ض¹£®شعشث¶¯¹³جضذ£¬
ح£ض¹£®شعشث¶¯¹³جضذ£¬
¢ظزرضھµم![]() µؤثظ¶بخھأ؟أë
µؤثظ¶بخھأ؟أë![]() £¬µم
£¬µم![]() µؤثظ¶بخھأ؟أë
µؤثظ¶بخھأ؟أë![]() £¬شث¶¯ت±¼نخھ
£¬شث¶¯ت±¼نخھ![]() أ룬µ±
أ룬µ±![]() ثؤµمخھ¶¥µمµؤثؤ±كذختائ½ذذثؤ±كذخت±£¬شٍ
ثؤµمخھ¶¥µمµؤثؤ±كذختائ½ذذثؤ±كذخت±£¬شٍ![]() ____________£®
____________£®
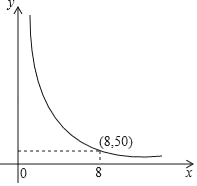
¢عبôµم![]() µؤشث¶¯آ·³ج·ض±ًخھ
µؤشث¶¯آ·³ج·ض±ًخھ![]() £¨µ¥خ»:
£¨µ¥خ»:![]() £©£¬زرضھ
£©£¬زرضھ![]() ثؤµمخھ¶¥µمµؤثؤ±كذختائ½ذذثؤ±كذخ£¬شٍ
ثؤµمخھ¶¥µمµؤثؤ±كذختائ½ذذثؤ±كذخ£¬شٍ![]() سë
سë![]() آْ×مµؤتء؟¹طدµت½خھ____________£®
آْ×مµؤتء؟¹طدµت½خھ____________£®
،¾´ً°¸،؟£¨1£©¼û½âخِ£»£¨2£©¢ظ![]() £»¢ع
£»¢ع![]()
،¾½âخِ،؟
(1)دبض¤أ÷ثؤ±كذخAFCEخھئ½ذذثؤ±كذخ£¬شظ¸ù¾ف¶ش½ادك»¥دà´¹ض±ئ½·ضµؤئ½ذذثؤ±كذختاءâذخ×÷³ِإذ¶¨£»
(2)¢ظ·ضاé؟ِجضآغ؟ةضھ£¬µ±PµمشعBFةد،¢QµمشعEDةدت±£¬²إؤـ¹¹³ةئ½ذذثؤ±كذخ£¬¸ù¾فئ½ذذثؤ±كذخµؤذشضتءذ³ِ·½³جاَ½â¼´؟ة£»
¢ع·ضبضضاé؟ِجضآغ؟ةضھaسëbآْ×مµؤتء؟¹طدµت½.
£¨1£©ض¤أ÷£؛،كثؤ±كذخ![]() تا¾طذخ£¬
تا¾طذخ£¬
،à![]()
،à![]() £¬
£¬
،ك![]() ´¹ض±ئ½·ض
´¹ض±ئ½·ض![]() £¬´¹×مخھ
£¬´¹×مخھ![]() £¬
£¬
،à![]() £¬
£¬
،à![]() £¬
£¬
،à![]() £¬
£¬
،àثؤ±كذخ![]() خھئ½ذذثؤ±كذخ£¬
خھئ½ذذثؤ±كذخ£¬
سض،ك![]()
،àثؤ±كذخ![]() خھءâذخ£¬
خھءâذخ£¬
£¨2£©¢ظ![]() أ룮
أ룮
دشب»µ±![]() µمشع
µمشع![]() ةدت±£¬
ةدت±£¬![]() µمشع
µمشع![]() ةد£¬´ثت±
ةد£¬´ثت±![]() ثؤµم²»؟ةؤـ¹¹³ةئ½ذذثؤ±كذخ£»ح¬ہي
ثؤµم²»؟ةؤـ¹¹³ةئ½ذذثؤ±كذخ£»ح¬ہي![]() µمشع
µمشع![]() ةدت±£¬
ةدت±£¬![]() µمشع
µمشع![]() »ٍ
»ٍةد£¬ز²²»ؤـ¹¹³ةئ½ذذثؤ±كذخ£®زٍ´ثض»سذµ±
![]() µمشع
µمشع![]() ةد،¢
ةد،¢![]() µمشع
µمشع![]() ةدت±£¬²إؤـ¹¹³ةئ½ذذثؤ±كذخ£®
ةدت±£¬²إؤـ¹¹³ةئ½ذذثؤ±كذخ£®
،àزش![]() ثؤµمخھ¶¥µمµؤثؤ±كذختائ½ذذثؤ±كذخت±£¬
ثؤµمخھ¶¥µمµؤثؤ±كذختائ½ذذثؤ±كذخت±£¬![]()
،àµم![]() µؤثظ¶بخھأ؟أë
µؤثظ¶بخھأ؟أë![]() £¬µم
£¬µم![]() µؤثظ¶بخھأ؟أë
µؤثظ¶بخھأ؟أë![]() £¬شث¶¯ت±¼نخھ
£¬شث¶¯ت±¼نخھ![]() أ룬
أ룬
،à![]() £¬
£¬
،à![]() £¬½âµأ
£¬½âµأ![]()
،àزش![]() ثؤµمخھ¶¥µمµؤثؤ±كذختائ½ذذثؤ±كذخت±£¬
ثؤµمخھ¶¥µمµؤثؤ±كذختائ½ذذثؤ±كذخت±£¬![]() أ룮
أ룮
¢ع![]() سë
سë![]() آْ×مµؤتء؟¹طدµت½تا
آْ×مµؤتء؟¹طدµت½تا![]() £¬
£¬
سةجâزâµأ£¬زش![]() ثؤµمخھ¶¥µمµؤثؤ±كذختائ½ذذثؤ±كذخت±£¬
ثؤµمخھ¶¥µمµؤثؤ±كذختائ½ذذثؤ±كذخت±£¬
µم![]() شع»¥دàئ½ذذµؤ¶شس¦±كةد£¬·ضبضضاé؟ِ£؛
شع»¥دàئ½ذذµؤ¶شس¦±كةد£¬·ضبضضاé؟ِ£؛
i£©بçح¼1£¬µ±![]() µمشع
µمشع![]() ةد،¢
ةد،¢![]() µمشع
µمشع![]() ةدت±£¬
ةدت±£¬![]() £¬¼´
£¬¼´![]() £¬µأ
£¬µأ![]() £®
£®
ii£©بçح¼2£¬µ±![]() µمشع
µمشع![]() ةد،¢
ةد،¢![]() µمشع
µمشع![]() ةدت±£¬
ةدت±£¬![]() £¬¼´
£¬¼´![]() £¬µأ
£¬µأ![]() £®
£®
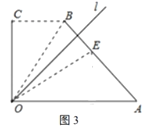
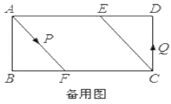
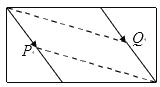
iii£©بçح¼3£¬µ±![]() µمشع
µمشع![]() ةد،¢
ةد،¢![]() µمشع
µمشع![]() ةدت±£¬
ةدت±£¬![]() £¬¼´
£¬¼´![]() £¬µأ
£¬µأ![]() £®
£®
×غةدثùتِ£¬![]() سë
سë![]() آْ×مµؤتء؟¹طدµت½تا
آْ×مµؤتء؟¹طدµت½تا![]() £®
£®

 شؤ¶ء؟ى³µدµءذ´ً°¸
شؤ¶ء؟ى³µدµءذ´ً°¸