题目内容
【题目】如图，在平面直角坐标系中，坐标原点为O，A点坐标为（4，0），B点坐标为（﹣1，0），以AB的中点P为圆心，AB为直径作⊙P的正半轴交于点C．
（1）求经过A、B、C三点的抛物线所对应的函数解析式；
（2）设M为（1）中抛物线的顶点，求直线MC对应的函数解析式；
（3）试说明直线MC与⊙P的位置关系，并证明你的结论．
【答案】（1）
（2）
（3）MC与⊙P的位置关系是相切
【解析】解：（1）∵A（4，0），B（－1，0），
∴AB=5，半径是PC=PB=PA=
。∴OP=
。
在△CPO中，由勾股定理得：
。∴C（0，2）。
设经过A、B、C三点抛物线解析式是
，
把C（0，2）代入得：
，∴
。
∴
。
∴经过A、B、C三点抛物线解析式是，
（2）∵
，∴M
。
设直线MC对应函数表达式是y=kx+b，
把C（0，2），M
代入得：
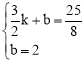，解得
。
∴直线MC对应函数表达式是。
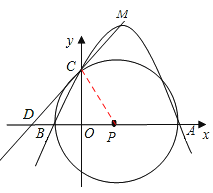
（3）MC与⊙P的位置关系是相切。证明如下：
设直线MC交x轴于D，
当y=0时，
，∴
，OD=
。∴D（
，0）。
在△COD中，由勾股定理得：
，
又
，
，
∴CD2+PC2=PD2。
∴∠PCD=900，即PC⊥DC。
∵PC为半径，
∴MC与⊙P的位置关系是相切。
（1）求出半径，根据勾股定理求出C的坐标，设经过A、B、C三点抛物线解析式是
，把C（0，2）代入求出a即可。
（2）求出M的坐标，设直线MC对应函数表达式是y=kx+b，把C（0，2），M
代入得到方程组，求出方程组的解即可。
（3）根据点的坐标和勾股定理分别求出PC、DC、PD的平方，根据勾股定理的逆定理得出∠PCD=900，即可作出判断。
练习册系列答案
相关题目
