题目内容
【题目】已知关于x的一元二次方程ax2+x+2=0.
(1)求证:当a<0时,方程ax2+x+2=0一定有两个不等的实数根;
(2)若代数式﹣x2+x+2的值为正整数,且x为整数时,求x的值;
(3)当a=a1时,抛物线y=ax2+x+2与x轴的正半轴相交于点M(m,0);当a=a2时,抛物线y=ax2+x+2与x轴的正半轴相交于点N(n,0);若点M在点N的左边,试比较a1与a2的大小.
【答案】(1)见解析;(2)x的值是0或1;(3)a1<a2.
【解析】
(1)求出b2﹣4ac的值,根据正负即可判断;
(2)求出原式=﹣(x2﹣x﹣2)的范围确定其整数为1或2,算出﹣x2+x+2=1和﹣x2+x+2=2的解即可;
(3)把a=a1,a=a1代入求出其值,求出a1﹣a2的值即可.
(1)△=1﹣8a.
∵a<0,∴﹣8a>0即:△>0,∴方程ax2+x+2=0一定有两个不等的实数根.
(2)原式=﹣(x2﹣x﹣2)=![]()
∵不论x为何值,﹣(x![]() )2≤0,∴原式=﹣(x
)2≤0,∴原式=﹣(x![]() )2
)2![]() .
.
∵代数式﹣x2+x+2的值为正整数,∴代数式﹣x2+x+2的值为1或2.
①当﹣x2+x+2=1时,这时x的值不是整数,不符合题意,舍去;
②当﹣x2+x+2=2时,解得:x=0或1.
答:x的值是0或1.
(3)∵当a=a1时,抛物线y=ax2+x+2与x轴的正半轴相交于点M(m,0),∴0=a1m2+m+2①.
∵当a=a2时,抛物线y=ax2+x+2与x轴的正半轴相交于点N(n,0),∴0=a2n2+n+2②,∴![]() ,∴
,∴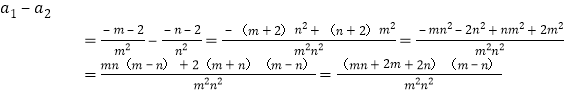 .
.
∵点M在点N的左边,且M、N均在x轴正半轴,∴m>0,n>0,m<n,∴mn+2m+2n>0,m﹣n<0,m2n2>0,∴a1﹣a2![]() ,∴a1<a2.
,∴a1<a2.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目