题目内容
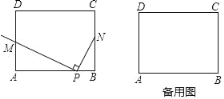
【题目】如图,在矩形ABCD中,AB=4,AD=3,点N为BC边上的一点,且BN=n(n>0),动点P从点A出发,以每秒1个单位长的速度沿AB边向点B运动,连接NP,作射线PM⊥NP交AD于点M,设点P运动的时间是t秒(t>0).
(1)当点M与点A重合时,t等于多少秒,当点M与点D重合时,n等于多少(用含字母t的代数式表示)
(2)若n=2,则
①在点P运动过程中,点M是否可以到达线段AD的延长线上?通过计算说明理由;
②连接ND,当t为何值时,ND∥PM?
(3)过点N作NK∥AB,交AD于点K,若在点P运动过程中,点K与点M不会重合,直接写出n的取值范围.
【答案】(1)t=4秒,点M与点A重合;n=﹣![]() ,(2)①点M不能到达线段AD的延长线上,理由见解析;②当t=
,(2)①点M不能到达线段AD的延长线上,理由见解析;②当t=![]() 秒时,ND∥PM,(3)2<n≤3.
秒时,ND∥PM,(3)2<n≤3.
【解析】
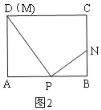
(1)当点M与点A重合时,如图1,AP=AP=4,可得t=4,当点M与点D重合时,如图2,利用三角形相似列比例式可得n的式子;
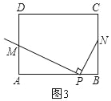
(2)①如图3,根据△AMP∽△BPN,列比例式![]() ,可得AM=
,可得AM=![]() t(4﹣t)=
t(4﹣t)=![]() =﹣
=﹣![]() (t﹣2)2+2,当t=2时,AM取得最大值为2,此时点M在线段AD上;
(t﹣2)2+2,当t=2时,AM取得最大值为2,此时点M在线段AD上;
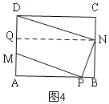
②如图4,作辅助线构建平行线,证明△PMA∽△NDQ,则![]() ,列方程可得t的值;
,列方程可得t的值;
(3)根据图4,点Q即为本题中的点K,由(2)①的解答过程可知,△AMP∽△BPN,则![]() ,当点K与点M重合时,则有AM=AK=BN=n,列方程t2﹣4t+n2=0,无解可得n的取值.
,当点K与点M重合时,则有AM=AK=BN=n,列方程t2﹣4t+n2=0,无解可得n的取值.
(1)当点M与点A重合时,P与B重合,N与C重合,如图1,
∴PA=AB=4,
∴t=4,
即t=4秒,点M与点A重合;
当点M与点D重合时,如图2,
∵∠DPN=90°,
∴∠APD+∠BPN=90°,
∵四边形ABCD是矩形,
∴∠A=∠B=90°,
∴∠ADP+∠APD=90°,
∴∠BPN=∠ADP,
∴△DAP∽△PBN,
![]() ,
,
![]()
![]() ,
,
故答案为:4,![]() ;
;
(2)①不能;
如图3,同理得:△AMP∽△BPN.
∴![]() ,
,
即![]() ,
,
∴AM=![]() t(4﹣t)=
t(4﹣t)=![]() ,
,
显然,AM是关于t的二次函数,当t=2时,AM取得最大值为2,此时点M在线段AD上,所以点M不能到达线段AD的延长线上.
②如图4,过点N作NQ∥AB,交AD于点Q,
∴∠PAM=∠NQD=90°,
当ND∥PM时,有∠PMA=∠NDQ,
∴△PMA∽△NDQ,
∴![]() ,
,
而PA=t,NQ=4,MA=![]() ,DQ=3﹣2=1,
,DQ=3﹣2=1,
代入得,![]() ,即2t2﹣
,即2t2﹣![]() t=0,解得,t1=0(舍去),t2=
t=0,解得,t1=0(舍去),t2=![]() .
.
∴当t=![]() 秒时,ND∥PM.
秒时,ND∥PM.
(3)2<n≤3.
理由是:如图4,点Q即为本题中的点K,由(2)①的解答过程可知,
∴△AMP∽△BPN.
∴![]() ,即
,即![]() ,
,
当点K与点M重合时,则有AM=AK=BN=n,
∴![]() ,化简得,t2﹣4t+n2=0,
,化简得,t2﹣4t+n2=0,
依题意,不存在点K与点M重合的时刻t,即关于t的一元二次方程t2﹣4t+n2=0无解,
∴△<0,即(﹣4)2﹣4×1×n2<0,n2>4,
∵n>0,
∴n>2,
综上,2<n≤3.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案【题目】为了传承中华优秀传统文化,某校组织八年级学生参加了“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解大赛的成绩分布情况,随机抽取了其中若干名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,绘制如下不完整的条形统计图.
汉字听写大赛成绩分数段统计表
分数段 | 频数 |
| 2 |
| 6 |
| 9 |
| 18 |
| 15 |
汉字听写大赛成绩分数段条形统计图

(1)补全条形统计图.
(2)这次抽取的学生成绩的中位数在________的分数段中;这次抽取的学生成绩在![]() 的分数段的人数占抽取人数的百分比是_______.
的分数段的人数占抽取人数的百分比是_______.
(3)若该校八年级一共有学生350名,成绩在90分以上(含90分)为“优”,则八年级参加这次比赛的学生中成绩“优”等的约有多少人?