Question

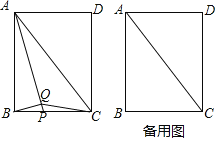
【题目】如图，在矩形ABCD中，AC为对角线，点P为BC边上一动点，连接AP，过点B作BQ⊥AP，垂足为Q，连接CQ．

⑴证明：△ABP∽△BQP；

⑵当点P为BC的中点时，若∠BAC＝37°，求∠CQP的度数；

⑶当点P运动到与点C重合时，延长BQ交CD于点F，若AQ＝AD，则等于多少．

Answer 1

【答案】（1）证明见解析；（2）∠CQP＝53°；（3）.

【解析】

（1）根据两角对应相等的两个三角形相似即可判断．

（2）只要证明△CPQ∽△APC，可得∠PQC＝∠ACP即可解决问题．

（3）连接AF．与Rt△ADF≌Rt△AQF（HL），推出DF＝QF，设AD＝AQ＝BC＝m，DF＝FQ＝x，FC＝y，CQ＝a，证明△BCQ∽△CFQ，可得，推出，即＝，由CF∥AB，可得，推出，可得，推出x2+xy﹣y2＝0，解得或（舍弃），由此即可解决问题．

（1）证明：∵四边形ABCD是矩形，

∴∠ABP＝90°，

∵BQ⊥AP，

∴∠BQP＝∠ABP＝90°，

∵∠BPQ＝∠APB，

∴△ABP∽△BQP．

（2）解：∵△ABP∽△BQP，

∴，

∴PB2＝PQPA，

∵PB＝PC，

∴PC2＝PQPA，

∴，

∵∠CPQ＝∠APC，

∴△CPQ∽△APC，

∴∠PQC＝∠ACP，

∵∠BAC＝37°，

∴∠ACB＝90°﹣37°＝53°，

∴∠CQP＝53°．

（3）解：连接AF．

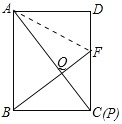
∵∠D＝∠AQF＝90°，AF＝AF，AD＝AQ，

∴Rt△ADF≌Rt△AQF（HL），

∴DF＝QF，设AD＝AQ＝BC＝m，DF＝FQ＝x，FC＝y，CQ＝a，

∵∠BCF＝∠CQB＝∠CQF＝90°，

∴∠BCQ+∠FCQ＝90°，∠∠CBQ＝90°，

∴∠FCQ＝∠CBQ，

∴△BCQ∽△CFQ，

,

,

,

∵CF∥AB，

,

,

,

∴x2+xy﹣y2＝0，

∴x＝y或y（舍弃），

,

,

故答案是：．