题目内容
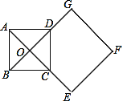
【题目】如图,正方形ABCD的对角线相交于点O,正方形OEFG的一边OG经过点D,且D是OG的中点,OG=![]() AB,若正方形ABCD固定,将正方形OEFG绕O点逆时针旋转α角,(0°<α<360°)得到正方形OE′F′G′,当α=__度时,∠OAG′=90°.
AB,若正方形ABCD固定,将正方形OEFG绕O点逆时针旋转α角,(0°<α<360°)得到正方形OE′F′G′,当α=__度时,∠OAG′=90°.
【答案】α的度数为30°或150°.
【解析】
根据题意和锐角正弦的概念以及特殊角的三角函数值得到∠AG′O=30°,分两种情况求出α的度数.
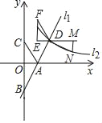
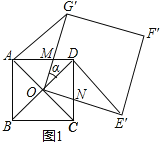
当α为锐角时,如图1所示:
∵四边形ABCD是正方形,
∴BC=AB,∠ABC=90°,OA=OD=![]() AC,
AC,
∴AC=![]() AB,
AB,
∵OG=![]() AB,
AB,
∴OG′=OG=AC=2AO,
∵∠OAG′=90°,OA=![]() OG′,
OG′,
∴∠AG′O=30°,
∴∠AOG′=60°,
∴∠DOG′=90°﹣60°=30°,即α=30°;
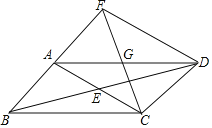
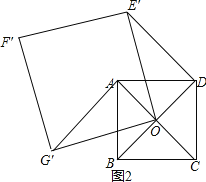
当旋转到如图2所示位置,同理证得∠AG′O=30°,
∴∠AOG′=60°,
∴α=90°+60°=150°,
综上所述:α的度数为30°或150°,
故答案为:30°或150°.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目