题目内容
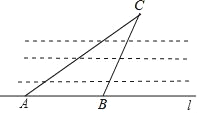
【题目】平行四边形ABOC在平面直角坐标系中,A、B的坐标分别为(﹣3,3),(﹣4,0).则过C的双曲线表达式为:_____.
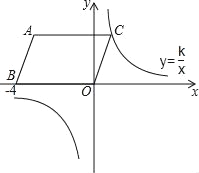
【答案】y=![]()
【解析】
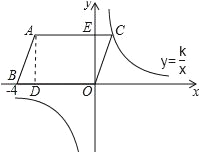
作AD⊥OB于D,先证明△ABD≌△OCE,得出BD=CE=1,AD=OE=3,得出点C坐标为(1,3),再设过C的双曲线表达式为:![]() ,把点C(1,3)代入求出k即可得出结果.
,把点C(1,3)代入求出k即可得出结果.
解:作AD⊥OB于D,如图所示:
则∠ADB=∠OEC=90°,
∵A、B的坐标分别为(﹣3,3),(﹣4,0),
∴OB=4,AD=3,OD=3,
∴BD=1,
∵四边形ABOC是平行四边形,
∴∠ABO=∠ACO,AB=OC,
在△ABD和△OCE中, 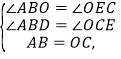
∴△ABD≌△OCE(AAS),
∴BD=CE=1,AD=OE=3,
∴C(1,3),
设过C的双曲线表达式为:![]() ,
,
把点C(1,3)代入得:k=3,
∴![]() ;
;
故答案为:![]() .
.

练习册系列答案
相关题目
【题目】为了传承中华优秀传统文化,某校组织八年级学生参加了“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解大赛的成绩分布情况,随机抽取了其中若干名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,绘制如下不完整的条形统计图.
汉字听写大赛成绩分数段统计表
分数段 | 频数 |
| 2 |
| 6 |
| 9 |
| 18 |
| 15 |
汉字听写大赛成绩分数段条形统计图

(1)补全条形统计图.
(2)这次抽取的学生成绩的中位数在________的分数段中;这次抽取的学生成绩在![]() 的分数段的人数占抽取人数的百分比是_______.
的分数段的人数占抽取人数的百分比是_______.
(3)若该校八年级一共有学生350名,成绩在90分以上(含90分)为“优”,则八年级参加这次比赛的学生中成绩“优”等的约有多少人?