题目内容
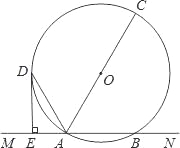
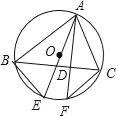
【题目】如图.PA和PB分别与⊙O相切于A,B两点,作直径AC,并延长交PB于点D.连结OP,CB.
(1)求证:OP∥CB;
(2)若PA=12,DB:DC=2:1,求⊙O的半径.

【答案】(1)证明见解析;(2)6.
【解析】
(1)PA和PB分别与⊙O相切于A、B两点,则满足切线长定理,易证AB⊥CB,根据AC是直径,可以得到∠ABC=90°,所以OP⊥AB,因而可以得到OP∥CB;
(2)由OP∥CB根据平行线分线段成比例定理,就可以得到![]() ,再根据PA=PB,从而求出OC即半径的长.
,再根据PA=PB,从而求出OC即半径的长.
(1)证明:连接AB,

∵PA、PB分别与⊙O相切于A、B两点,
∴PA=PB且∠APO=∠BPO,
∴OP⊥AB,
∵AC是⊙O的直径,
∴∠ABC=90°,
∴AB⊥CB,
OP∥CB;
(2)∵由(1)知OP∥CB,
∴![]() ,
,
又∵PB=PA=12,![]() ,
,
∴![]() ,
,
∴OC=6.
即⊙O的半径为6.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目