题目内容
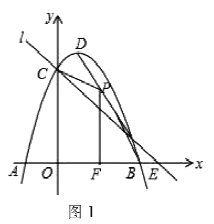
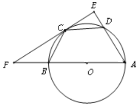
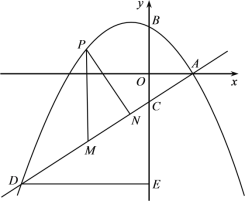
【题目】如图,抛物线![]() 与
与![]() 轴交于点A(2,0),交
轴交于点A(2,0),交![]() 轴于点B(0,
轴于点B(0,![]() ),直线
),直线![]() 过点A与y轴交于点C,与抛物线的另一个交点为D,作DE⊥y轴于点E.设点P是直线AD上方的抛物线上一动点(不与点A、D重合),过点P作y轴的平行线,交直线AD于点M,作PN⊥AD于点N.
过点A与y轴交于点C,与抛物线的另一个交点为D,作DE⊥y轴于点E.设点P是直线AD上方的抛物线上一动点(不与点A、D重合),过点P作y轴的平行线,交直线AD于点M,作PN⊥AD于点N.
⑴填空:![]() = ,
= ,![]() = ,
= ,![]() = ;
= ;
⑵探究:是否存在这样的点P,使四边形PMEC是平行四边形?若存在,请求出点P的坐标;若不存在,请说明理由;
⑶设△PMN的周长为![]() ,点P的横坐标为x,求
,点P的横坐标为x,求![]() 与x的函数关系式,并求出
与x的函数关系式,并求出![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)点P的坐标是(-2,3)和(-4,1.5);(3)当x=-3时,
;(2)点P的坐标是(-2,3)和(-4,1.5);(3)当x=-3时,![]() 的最大值是15.
的最大值是15.
【解析】
(1)将A,B两点代入![]() 可求出b,c的值,将A点代入
可求出b,c的值,将A点代入![]() 可求出k的值;
可求出k的值;
(2)设出P,M点的坐标,从而得出PM的长,将两函数联立得出点D坐标,可得出CE的长,利用平行四边形的性质可知PM=CE,列出方程求解即可;
(3)利用勾股定理得出DC的长,根据△PMN∽△DCE,得出两三角形周长之比等于相似比,从而得出l与x的函数关系,再利用配方法求出二次函数最值即可.
解:⑴
因为抛物线![]() 经过点A(2,0),B(0,
经过点A(2,0),B(0,![]() ),代入抛物线解析式可得:
),代入抛物线解析式可得:
 ,解得
,解得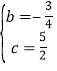 ,所以抛物线解析式为
,所以抛物线解析式为![]() ,因为直线
,因为直线
![]() 经过点A(2,0),代入直线解析式得:
经过点A(2,0),代入直线解析式得:![]() ,解得:
,解得:![]() ,所以直线解析式为:
,所以直线解析式为:![]() ,所以
,所以![]() ;
;
⑵ 存在;
设P的坐标是(x,![]() ),则M的坐标是(x,
),则M的坐标是(x,![]() ,)
,)
∴![]() ,
,
解方程 得:
得: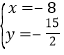 ,
,![]() ,
,
∵点D在第三象限,则点D的坐标是(-8,-7.5),
由y=![]() 得点C的坐标是(0,-1.5),
得点C的坐标是(0,-1.5),
∴CE=-1.5-(-7.5)=6,
由于PM∥y轴,所以当PM=CE时四边形PMEC是平行四边形。
即![]() =6,
=6,
解这个方程得:x1=-2,x2=-4,符合-8<x<2,
当x=-2时,y=3,当x=-4时,y=1.5,
综上所述:点P的坐标是(-2,3)和(-4,1.5);
⑶ 在Rt△CDE中,DE=8,CE=6 由勾股定理得:![]() ,
,
∴△CDE的周长是24,
∵PM∥y轴,∴△PMN∽△DCE,
∴![]() ,即
,即![]() 化简整理得:l与x的函数关系式是:
化简整理得:l与x的函数关系式是:
![]() ,
,
因为![]() ,∴当x=-3时,
,∴当x=-3时,![]() 的最大值是15.
的最大值是15.


 阅读快车系列答案
阅读快车系列答案【题目】光明中学全体学生900人参加社会实践活动,从中随机抽取50人的社会实践活动成绩制成如图所示的条形统计图,结合图中所给信息解答下列问题:
![]() 填写下表:
填写下表:
中位数 | 众数 | |
随机抽取的50人的社会实践活动成绩 |
![]() 估计光明中学全体学生社会实践活动成绩的总分.
估计光明中学全体学生社会实践活动成绩的总分.