Question

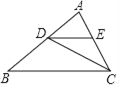
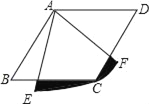
【题目】如图，四边形ABCD是菱形，∠B＝60°，AB＝1，扇形AEF的半径为1，圆心角为60°，则图中阴影部分的面积是_____．

Answer 1

【答案】

【解析】

根据菱形的性质得出△ADC和△ABC是等边三角形，进而利用全等三角形的判定得出△ADH≌△ACG，得出四边形AGCH的面积等于△ADC的面积，进而求出即可．

连接AC，

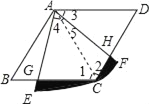
∵四边形ABCD是菱形，

∴∠B=∠D=60°，AB=AD=DC=BC=1，

∴∠BCD=∠DAB=120°，

∴∠1=∠2=60°，

∴△ABC、△ADC都是等边三角形，

∴AC=AD=1，

∵AB=1，

∴△ADC的高为，AC=1，

∵扇形BEF的半径为1，圆心角为60°，

∴∠4+∠5=60°，∠3+∠5=60°，

∴∠3=∠4，

设AF、DC相交于HG，设BC、AE相交于点G，

在△ADH和△ACG中，

，

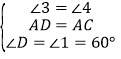∴△ADH≌△ACG(ASA)，

∴四边形AGCH的面积等于△ADC的面积，

∴图中阴影部分的面积是：S扇形AEF﹣S△ACD==，

故答案为：．