题目内容
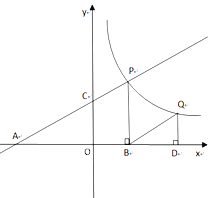
【题目】如图,直线y=![]() x+3分别交 x轴、y轴于点A、C.点P是该直线与双曲线在第一象限内的一个交点,PB⊥x轴于B,且S△ABP=16.
x+3分别交 x轴、y轴于点A、C.点P是该直线与双曲线在第一象限内的一个交点,PB⊥x轴于B,且S△ABP=16.
(1)求证:△AOC∽△ABP;
(2)求点P的坐标;
(3)设点Q与点P在同一个反比例函数的图象上,且点Q在直线PB的右侧,作QD⊥x轴于D,当△BQD与△AOC相似时,求点Q的横坐标.
【答案】(1)证明见解析;(2)点P的坐标为(2,4);(3)点Q的横坐标为:![]() 或
或![]() .
.
【解析】
(1)利用PB∥OC,即可证明三角形相似;
(2)由一次函数解析式,先求点A、C的坐标,由△AOC∽△ABP,利用线段比求出BP,AB的值,从而可求出点P的坐标即可;
(3)把P坐标代入求出反比例函数,设Q点坐标为(n,![]() ),根据△BQD与△AOC相似分两种情况,利用线段比联立方程组求出n的值,即可确定出Q坐标.
),根据△BQD与△AOC相似分两种情况,利用线段比联立方程组求出n的值,即可确定出Q坐标.
(1)证明:∵PB⊥ x轴,OC⊥x轴,
∴OC∥PB,
∴△AOC∽△ABP;
(2)解:对于直线y=![]() x+3,
x+3,
令x=0,得y=3;
令 y=0,得x=-6 ;
∴A(-6,0),C(0,4),
∴OA=6,OC=3.
∵△AOC∽△ABP,
∴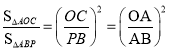 ,
,
∵S△ABP=16,S△AOC=![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴PB=4,AB=8,
∴OB=2,
∴点P的坐标为:(2,4).
(3)设反比例函数的解析式为:y=![]() ,
,
把P(2,4)代入,得k=xy=2×4=8,
∴y=![]() .
.
点Q在双曲线上,可设点Q的坐标为:(n,![]() )(n>2),
)(n>2),
则BD=![]() ,QD=
,QD=![]() ,
,
①当△BQD∽△ACO时,![]() ,
,
即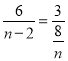 ,
,
整理得:![]() ,
,
解得:![]() 或
或![]() ;
;
②当△BQD∽△CAO时,![]() ,
,
即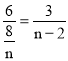 ,
,
整理得:![]() ,
,
解得:![]() ,
,![]() (舍去),
(舍去),
综上①②所述,点Q的横坐标为:1+![]() 或1+
或1+![]() .
.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目