题目内容
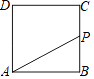
【题目】如图,已知在正方形ABCD外取一点E,连接CE、BE、DE.过点C作CE的垂线交BE于点F.CE=CF=1,DF= ![]() .下列结论:①△BCF≌△DCE;②EB⊥ED;③点D到直线CE的距离为2;④S四边形DECF=
.下列结论:①△BCF≌△DCE;②EB⊥ED;③点D到直线CE的距离为2;④S四边形DECF= ![]() +
+ ![]() .其中正确结论的序号是 .
.其中正确结论的序号是 . 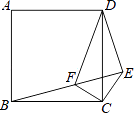
【答案】①②④
【解析】解:在正方形ABCD中,
BC=CD,∠BCD=90°,
∵∠EACF90°,
∴∠BCF=∠DCE,
在△BCF与△DCE中,
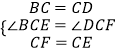 ,
,
∴△BCE≌△DCF(SAS),
故①正确;
∵△BCF≌△DCE,
∴∠CBF=∠CDE,
∴∠DEB=∠BCD=90°,
∴BE⊥ED,
故②正确,
过点D作DM⊥CE,交CE的延长线于点M,
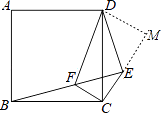
∵∠ECF=90°,
FC=EC=1,
∴∠CEF=45°,
∵∠DEM+∠CEB=90°,
∴∠DEM=∠EDM=45°,
∴EM=DM,
∴由勾股定理可求得:EF= ![]() ,
,
∵DF= ![]() ,
,
∴由勾股定理可求得:DE=2,
∵EF2+BF2=2BF2=BE2,
∴DM=EM= ![]() ,故③错误,
,故③错误,
∵△BCF≌△ADCE,
∴S△BCF=S△DCE,
∴S△DCE+S△DCF
=S△ECF+S△DEF
=S△AEP+S△PEB
= ![]() +
+ ![]() ,故④正确,
,故④正确,
所以答案是①②④
【考点精析】本题主要考查了正方形的性质的相关知识点,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题.

【题目】观察下表三行数的规律,回答下列问题:
第1列 | 第2列 | 第3列 | 第4列 | 第5列 | 第6列 | … | |
第1行 | -2 | 4 | -8 | a | -32 | 64 | … |
第2行 | 0 | 6 | -6 | 18 | -30 | 66 | … |
第3行 | -1 | 2 | -4 | 8 | -16 | b | … |
(1)第1行的第四个数a是 ;第3行的第六个数b是 ;
(2)若第1行的某一列的数为c,则第2行与它同一列的数为 ;
(3)已知第n列的三个数的和为2562,若设第1行第n列的数为x,试求x的值.