题目内容
【题目】如图,在平面直角坐标系xOy中,直线y1=﹣x+b过点A,且与直线y2=x+3相交于点B(m,2),直线y2=x+3与x轴相交于点C. 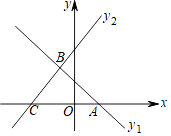
(1)求m的值.
(2)求△ABC的面积.
(3)根据图象,直接写出关于x的不等式﹣x+b>x+3的解集.
【答案】
(1)解:∵直线y2=x+3过点B(m,2),
∴2=m+3,
解得:m=﹣1.

(2)解:∵直线y1=﹣x+b过点B(﹣1,2),
∴2=1+b,
解得:b=1,
∴直线y1的解析式为y1=﹣x+1.
当y1=﹣x+1=0时,x=1,
∴点A的坐标为(1,0);
当y2=x+3=0时,x=﹣3,
∴点C的坐标为(﹣3,0),
∴BC=1﹣(﹣3)=4,
∴S△ABC= ![]() ACyB=
ACyB= ![]() ×4×2=4.
×4×2=4.
(3)解:观察函数图象,可知:当x<﹣1时,直线y1在直线y2的上方,
∴不等式﹣x+b>x+3的解集为x<﹣1.
【解析】(1)由点B的坐标利用一次函数图象上点的坐标特征可求出m值;(2)由点B的坐标利用一次函数图象上点的坐标特征可求出b的值,再利用一次函数图象上点的坐标特征可求出点A、C的值,由点A、B、C的坐标利用三角形的面积可求出△ABC的面积;(3)根据两直线的上下位置关系结合点B的横坐标,即可得出不等式的解集.
【考点精析】关于本题考查的三角形的面积,需要了解三角形的面积=1/2×底×高才能得出正确答案.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目