Question

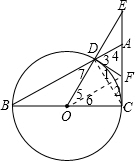
如图，在Rt△ABC中，∠C=90°，以BC边为直径的⊙O交AB于点D，连接OD并延长交CA的延长线于点E，过点D作DF⊥OE交EC于点F．
（1）求证：AF=CF．
（2）若ED=2，sin∠E=

3

5

，求AD的长．

Answer 1

（1）证法一：连接CD，OC、OD为⊙O的半径，
且OC⊥EC，DF⊥OE
∴FD、FC为⊙O的两条切线
．∴FD=FC
∴∠1=∠2．
又∵BC为⊙O的直径，
∴∠BDC=90°
∴∠CDA=180°-90°=90°．
在Rt△CAD中，∠1+∠3=90°，∠2+∠4=90°
又∵∠1=∠2．∠3=∠4．
∴FD=FA
又FD=FC．
∴AF=CF．
证法二：连接OF，证明FD=FC的步骤同证法一．
∵FC⊥OC，FD⊥OD∴
OF为∠COD的平分．
∠5=∠6．
又∵∠5+∠6=∠7+∠B，OB=OD
∴∠7=∠B．
∴2∠5=2∠7
∴∠5=∠7．
∴OF∥BA．
∵O为BC的中点．
∴AF=CF．

（2）设⊙O的半径为R，在Rt△OCE中，OE=OD+DE=R+2，
sin∠E=

R

R+2

，由sin∠E=

3

5

得R=3
在Rt△EDF中，siN∠E=

3

5

，ED=2．设DF=3k，EF=5k，
根据勾股定理，得（3k）²+22=（5k）²，
解得k=

1

2

∴DF=

3

2

，EF=

5

2

∴AC=2AF=2DF=3．
在Rt△ABC中，AB=3

5

∵AC和ADB分别为⊙O的切线和割线，
∴AC²=AD•AB，
解得AD=

3 5

5

．