题目内容
如图,在直角梯形ABCD中,AD∥BC,∠ABC= 900,中位线EF分别交BD,AC于点G,H,∠ACB=300,则下列结论中正确的有______.(填序号)
①EG+ HF =AD;②AO ? OB=CO?OD,
③BC -AD =2GH; ④△ABH是等边三角形
①EG+ HF =AD;②AO ? OB=CO?OD,
③BC -AD =2GH; ④△ABH是等边三角形

①②③④
(1)∵中位线EF分别交BD,AC于点G,H∴EG、HF分别是△ABD、△ACD的中位线,
∴EG= AD,HF=
AD,HF= AD∴EG+HF=AD
AD∴EG+HF=AD
(2)∵AD∥BC∴△AOD∽△COB∴ ,即AO•OB=CO•OD
,即AO•OB=CO•OD
(3)∵中位线EF分别交BD,AC于点G,H∴FG、HF分别是△CBD、△ACD的中位线
∴FG= BC,HF=
BC,HF= AD∴GH=FG-HF=
AD∴GH=FG-HF= (BC-AD)∴BC-AD=2GH
(BC-AD)∴BC-AD=2GH
(4)∵EH∥BC,AE=EB∴AH=HC∴在Rt△ABC中,BH=AH
又∵∠ACB=30°∴∠BAC=60°∴△ABH是等边三角形.故全部正确.
∴EG=
 AD,HF=
AD,HF= AD∴EG+HF=AD
AD∴EG+HF=AD(2)∵AD∥BC∴△AOD∽△COB∴
 ,即AO•OB=CO•OD
,即AO•OB=CO•OD(3)∵中位线EF分别交BD,AC于点G,H∴FG、HF分别是△CBD、△ACD的中位线
∴FG=
 BC,HF=
BC,HF= AD∴GH=FG-HF=
AD∴GH=FG-HF= (BC-AD)∴BC-AD=2GH
(BC-AD)∴BC-AD=2GH(4)∵EH∥BC,AE=EB∴AH=HC∴在Rt△ABC中,BH=AH
又∵∠ACB=30°∴∠BAC=60°∴△ABH是等边三角形.故全部正确.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目

 中,
中, 为边
为边 的中点,且
的中点,且 交于点
交于点 ,那么
,那么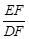 =_______.
=_______.


 轴于点F(如图).设动点P、Q运动时间为t(单位:秒),则:
轴于点F(如图).设动点P、Q运动时间为t(单位:秒),则: