Question

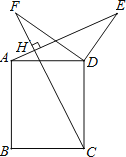
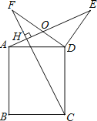
【题目】如图，四边形ABCD是矩形，点E、F是矩形ABCD外两点，AE⊥CF于H，AD=3,DC=4,DE=,∠EDF=90°,则DF的长是（ ）

A.B.C.D.

Answer 1

【答案】A

【解析】

设DF和AE相交于O点，由矩形的性质和已知条件可证明∠E=∠F，∠ADE=∠FDC，进而可得到△ADE∽△CDF，由相似三角形的性质：对应边的比值相等即可求出DF的长．

解：设DF和AE相交于O点，

∵四边形ABCD是矩形，
∴∠ADC=90°，
∵∠EDF=90°，
∴∠ADC+∠FDA=∠EDF+∠FDA，
即∠FDC=∠ADE，
∵AE⊥CF于点H，
∴∠F+∠FOH=90°，
∵∠E+∠EOD=90°，∠FOH=∠EOD，
∴∠F=∠E，
∴△ADE∽△CDF，
∴AD：CD=DE：DF，

故选：A．