Question

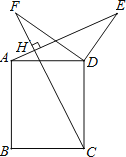
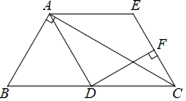
【题目】如图，在矩形ABCD中，点E是AD上的一个动点，连接BE，作点A关于BE的对称点F，且点F落在矩形ABCD的内部，连结AF、BF、EF，过点F作GF⊥AF交AD于点G，设AD：AE＝n．

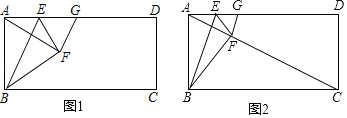
（1）线段AE和线段EG的数量关系是：　 　；

（2）如图②，当点F落在AC上时，用含n的代数式表示AD：AB的值；

（3）若AD＝4AB，且△FCG为直角三角形，求n的值．（直接写出结果）．

Answer 1

【答案】（1）AE＝EG；（2）；（3）n=16或n＝8+4

【解析】

（1）直接利用等角的余角相等得出∠FGA＝∠EFG，即可得出EG＝EF，代换即可；

（2）先判断出△ABE∽△DAC，得出比例式用AB＝DC代换化简即可得出结论；

（3）先判断出只有∠CFG＝90°或∠CGF＝90°，分两种情况建立方程求解即可．

解：设AE＝a，则AD＝na，

（1）由对称知，AE＝FE，

∴∠EAF＝∠EFA，

∵GF⊥AF，

∴∠EAF+∠FGA＝∠EFA+∠EFG＝90°，

∴∠FGA＝∠EFG，

∴EG＝EF，

∴AE＝EG，

故答案为：AE＝EG；

（2）如图1，当点F落在AC上时，

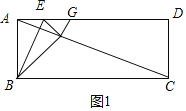
由对称知，BE⊥AF，

∴∠ABE+∠BAC＝90°，

∵∠DAC+∠BAC＝90°，

∴∠ABE＝∠DAC，

∵∠BAE＝∠D＝90°，

∴△ABE∽△DAC，

∵AB＝DC，

∴AB2＝ADAE＝na2，

∵AB＞0，

∴AB＝a，

（3）若AD＝4AB，则AB＝

如图2，当点F落在线段BC上时，

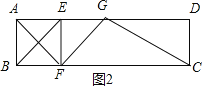
EF＝AE＝AB＝a，此时＝a，

∴n＝4，

∴当点F落在矩形内部时，n＞4，

∵点F落在矩形内部，点G在AD上，

① 当时，如图3，

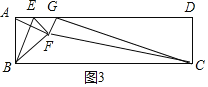
则点F落在AC上，由（2）得，

②当时,∠CGD+∠AGF＝90°，

∵∠FAG+∠AGF＝90°，

∴∠CGD＝∠FAG＝∠ABE，

∵∠BAE＝∠D＝90°，

∴△ABE∽△DGC，

∴ABDC＝DGAE，

∵DG＝AD﹣AE﹣EG＝na﹣2a＝（n﹣2）a，

∴（）2＝（n﹣2）aa，

∴n＝或n＝（由于n＞4，所以舍），

即：n＝8+4

综上所述，当或n＝8+4时，△FCG为直角三角形.