题目内容
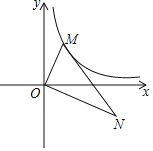
【题目】如图，在平面直角坐标系中，点M、N分别为反比例函数y＝
和y＝
的图象上的点，顺次连接M、O、N，∠MON＝90°，∠ONM＝30°，则k＝_____．
【答案】-6．
【解析】
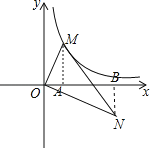
分别过M，N作MA⊥x轴于A，NB⊥x轴于B，根据30°的正切函数值得到
=tan30°＝
，根据相似三角形的判定证得△MOA∽△ONB，得到BN＝
OA，OB＝MA，由k的几何意义k＝﹣BNOB＝﹣3OAMA＝﹣3×2＝﹣6；
解：分别过M，N作MA⊥x轴于A，NB⊥x轴于B，
∵∠MON＝90°，∠ONM＝30°，
∴ =tan30°＝，
∵N在第四象限，
∴k＜0，∵∠BON＝∠OMA＝90°﹣∠MOA，∠MAO＝∠OBN＝90°，
∴△MOA∽△ONB，
∴
＝，
∴BN＝OA，OB＝MA，
∴k＝﹣BNOB＝﹣3OAMA＝﹣3×2＝﹣6，
故答案为：﹣6．
练习册系列答案
阅读快车系列答案
相关题目
【题目】阳光市场某个体商户购进某种电子产品，每个进价50元．调查发现，当售价为80元时，平均一周可卖出160个，而当每售价每降低2元时，平均一周可多卖出20个．若设每个电子产品降价x元，
（1）根据题意，填表：
进价（元） | 售价（元） | 每件利润（元） | 销量（个） | 总利润（元） | |
降价前 | 50 | 80 | 30 | 160 |
|
降价后 | 50 | ________ | ________ | ________ | ________ |
（2）若商户计划每周盈利5200元，且尽量减少库存，则每个电子产品应降价多少元？
