题目内容
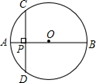
如图,⊙O的直径AB垂直于弦CD,垂足P是OB的中点,CD=6 ,求直径AB的长.
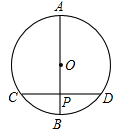

连OC,如图,
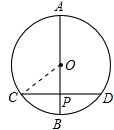
∵AB垂直于弦CD,
∴PC=PD,
而CD=6,
∴PC=3,
又∵P是OB的中点,
∴OC=2OP,
∴∠C=30°,
∴PC=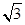 OP,则OP=
OP,则OP=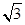 ,
,
∴OC=2OP=2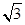 ,
,
所以直径AB的长为4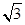

∵AB垂直于弦CD,
∴PC=PD,
而CD=6,
∴PC=3,
又∵P是OB的中点,
∴OC=2OP,
∴∠C=30°,
∴PC=
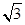 OP,则OP=
OP,则OP=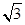 ,
,∴OC=2OP=2
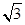 ,
,所以直径AB的长为4
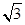
连OC,AB垂直于弦CD,由垂径定理得到PC=PD,得到PC=3;由P是OB的中点,则OC=2OP,得∠C=30°,PC=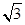 OP,则OP=
OP,则OP=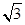 ,即可得到OC,AB
,即可得到OC,AB
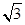 OP,则OP=
OP,则OP=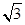 ,即可得到OC,AB
,即可得到OC,AB
练习册系列答案
 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
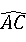 =
=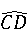 ,∠COD=60°
,∠COD=60°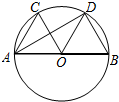
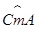 上异于点C、A的一点,若∠ABO=32°,则∠ADC的度数是
上异于点C、A的一点,若∠ABO=32°,则∠ADC的度数是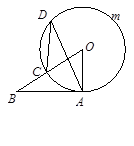
 为
为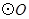 的内接三角形,
的内接三角形,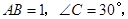 则
则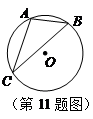
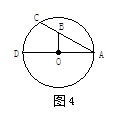
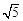 .求⊙O1的半径.
.求⊙O1的半径.