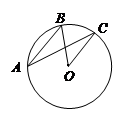题目内容
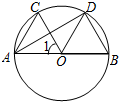
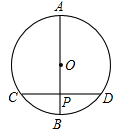
如图,AB是⊙O的直径,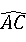 =
=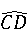 ,∠COD=60°
,∠COD=60°
(1)△AOC是等边三角形吗?请说明理由;(2)求证:OC∥BD.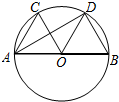
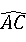 =
=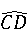 ,∠COD=60°
,∠COD=60°(1)△AOC是等边三角形吗?请说明理由;(2)求证:OC∥BD.

(1)△AOC是等边三角形,理由见解析(2)见解析
解:(1)△AOC是等边三角形 …………… 1分
证明:如图∵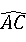 =
=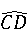 ,
,
∴∠1=∠COD=60° …………… 2分
∵OA=OC(⊙O的半径),
∴△AOC是等边三角形; ……………4分
(2)证法一:∵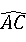 =
=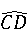 ,
,
∴OC⊥AD …………… 5分
又∵AB是⊙O的直径,
∴∠ADB=90°,即BD⊥AD …………… 6分
∴OC∥BD…………… 7分
证法二:∵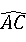 =
=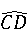 ,
,
∴∠1=∠COD=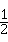 ∠AOD ……… 5分
∠AOD ……… 5分
又∠B=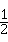 ∠AOD
∠AOD
∴∠1=∠B …… 6分
∴OC∥BD …… 7分
(1)由等弧所对的圆心角相等推知∠1=∠COD=60°;然后根据圆上的点到圆心的距离都等于圆的半径知OA=OC,从而证得△AOC是等边三角形;
(2)证法一:利用同垂直于一条直线的两条直线互相平行来证明OC∥BD;
证法二:通过证明同位角∠1=∠B,推知OC∥BD.
证明:如图∵
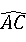 =
=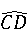 ,
,
∴∠1=∠COD=60° …………… 2分
∵OA=OC(⊙O的半径),
∴△AOC是等边三角形; ……………4分
(2)证法一:∵
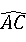 =
=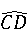 ,
,∴OC⊥AD …………… 5分
又∵AB是⊙O的直径,
∴∠ADB=90°,即BD⊥AD …………… 6分
∴OC∥BD…………… 7分
证法二:∵
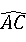 =
=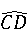 ,
,∴∠1=∠COD=
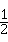 ∠AOD ……… 5分
∠AOD ……… 5分又∠B=
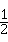 ∠AOD
∠AOD∴∠1=∠B …… 6分
∴OC∥BD …… 7分
(1)由等弧所对的圆心角相等推知∠1=∠COD=60°;然后根据圆上的点到圆心的距离都等于圆的半径知OA=OC,从而证得△AOC是等边三角形;
(2)证法一:利用同垂直于一条直线的两条直线互相平行来证明OC∥BD;
证法二:通过证明同位角∠1=∠B,推知OC∥BD.

练习册系列答案
相关题目





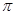 )
)