题目内容
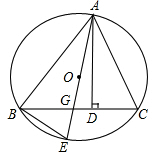
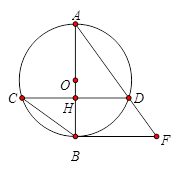
如图,AB为⊙O的直径,弦CD⊥AB于点H,过点B作⊙O的切线与AD的延长线交于F.
(1)求证: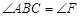
(2)若sinC=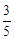 ,DF=6,求⊙O的半径.
,DF=6,求⊙O的半径.
(1)求证:
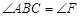
(2)若sinC=
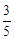 ,DF=6,求⊙O的半径.
,DF=6,求⊙O的半径.
(1)证明见解析;(2)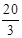 .
.
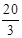 .
.试题分析:(1)一方面由切线的性质和平行的性质得到∠ADC=∠F四边形2另一方面由圆周角定理得∠ABC=∠ADC,从而证得∠ABC=∠F.
(2)连接BD,根据直径所对的圆周角为直角得到∠ADB=90°,根据切线的性质得到∠ABF=90°,利用锐角三角函数定义,在Rt△DBF中,由
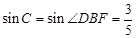 ,DF=6求得BD=8;在Rt△ABD中,由
,DF=6求得BD=8;在Rt△ABD中,由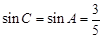 求得
求得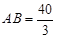 ,即可得到⊙O的半径.
,即可得到⊙O的半径.试题解析:(1)∵BF为⊙O的切线,∴AB⊥BF于点B.
∵ CD⊥AB,∴∠ABF =∠AHD =90°.
∴CD∥BF.∴∠ADC=∠F.
又∵∠ABC=∠ADC,∴∠ABC=∠F.
(2)如图,连接BD.
∵AB为⊙O的直径,∴∠ADB =90°.
由(1)∠ABF =90°,∴∠A=∠DBF.
又∵∠A=∠C,∴∠C=∠DBF.
在Rt△DBF中,
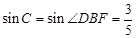 ,DF=6,∴BD=8.
,DF=6,∴BD=8.在Rt△ABD中,
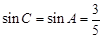 ,∴
,∴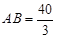 .∴⊙O的半径为
.∴⊙O的半径为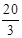 .
.

练习册系列答案
相关题目
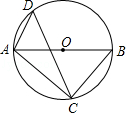
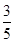 ,BP=6,AP=1,求QC的长.
,BP=6,AP=1,求QC的长.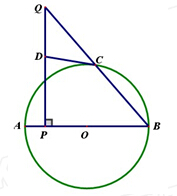
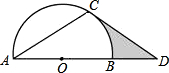
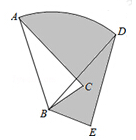
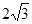 ,将△ABC绕点B顺时针旋转60°后得到△DBE,点A经过的路径为弧AD,则图中阴影部分的面积是 .
,将△ABC绕点B顺时针旋转60°后得到△DBE,点A经过的路径为弧AD,则图中阴影部分的面积是 .