题目内容
如图,C、D是线段AB上任意两点,E是线段AC的中点,F是线段BD的中点,若
EF=a,CD=b,求AB的长.
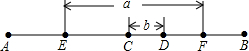
EF=a,CD=b,求AB的长.
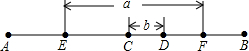
∵E是AC中点,F是BD中点,
∴AE=EC,DF=FB,
又∵EF=a,CD=b
∴EC+DF=EF-CD=a-b,
∴AE+FB=EC+DF=a-b,
∴AB=AE+EF+FB=(AE+FB)+EF
=a-b+a
=2a-b.
即AB=2a-b.
∴AE=EC,DF=FB,
又∵EF=a,CD=b
∴EC+DF=EF-CD=a-b,
∴AE+FB=EC+DF=a-b,
∴AB=AE+EF+FB=(AE+FB)+EF
=a-b+a
=2a-b.
即AB=2a-b.

练习册系列答案
相关题目