题目内容
已知，如图，四边形ABCD是正方形，E、F分别是AB和AD延长线上的点，且BE=DF，则∠CEF=______．
∵四边形ABCD是正方形，
∴CD=BC，∠CDF=∠CBE=90°，
在△CDF和△CBE中
，
∴△CDF≌△CBE，
∴CF=CE，∠DCF=∠BCE．
∵∠DCE+∠BCE=90°，
∴∠DCF+∠BCE=90°．
即∠FCE=90°，
∴△FEC是等腰直角三角形．
∴∠CEF=45°．
故答案为：45°．
∴CD=BC，∠CDF=∠CBE=90°，
在△CDF和△CBE中
|
∴△CDF≌△CBE，
∴CF=CE，∠DCF=∠BCE．
∵∠DCE+∠BCE=90°，
∴∠DCF+∠BCE=90°．
即∠FCE=90°，
∴△FEC是等腰直角三角形．
∴∠CEF=45°．
故答案为：45°．
练习册系列答案
相关题目
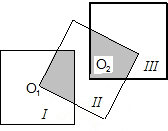
缘上，且P点在裁下的正方形一边上，问如何剪裁使得该正方形面积最大，最大面积是多少？