题目内容
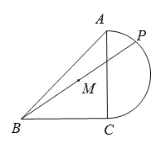
【题目】如图,在等腰直角ABC 中,斜边 AB 的长度为 8,以 AC 为直径作圆,点P 为半圆上的动点,连接 BP ,取 BP 的中点 M ,则CM 的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
连接AP、CP,分别取AB、BC的中点E、F,连接EF、EM和FM,根据三角形中位线的性质、圆周角定理的推论可得点M的运动轨迹为以EF为直径的半圆上,取EF的中点O,连接OC,点O即为半圆的圆心,从而得出当O、M、C共线时,CM最小,如图所示,CM最小为CM1的长,最后根据勾股定理求值即可.
解:连接AP、CP,分别取AB、BC的中点E、F,连接EF、EM和FM,
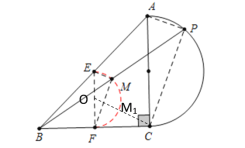
∴EM、FM和EF分别是△ABP、△CBP和△ABC的中位线
∴EM∥AP,FM∥CP,EF∥AC,EF=![]()
∴∠EFC=180°-∠ACB=90°
∵AC为直径
∴∠APC=90°,即AP⊥CP
∴EM⊥MF,即∠EMF=90°
∴点M的运动轨迹为以EF为直径的半圆上
取EF的中点O,连接OC,点O即为半圆的圆心
当O、M、C共线时,CM最小,如图所示,CM最小为CM1的长,
∵等腰直角ABC 中,斜边 AB 的长度为 8,
∴AC=BC=![]() =
=![]()
∴EF=![]() =
=![]() ,FC=
,FC=![]() =
=![]() ,
,
∴OM1=OF=![]() =
=![]()
根据勾股定理可得OC=![]()
∴CM1=OC-OM1=![]()
即CM最小值为![]()
故选C.

练习册系列答案
相关题目