Question

【题目】已知：如图，在△ABC中，AB=AC，∠A=36°．

（1）尺规作图：作AB的垂直平分线MN交AC于点D，连接BD；（保留作图痕迹，不写作法）

（2）求∠DBC的度数。

Answer 1

【答案】（1）答案见解析；（2）36°

【解析】

（1）分别以A、B点为圆心，以大于AB的长为半径作弧，两弧相交于M，N两点；作直线MN，即MN为线段AB的垂直平分线；

（2）由AB的垂直平分线MN交AC于D，根据线段垂直平分线的性质，即可求得AD=BD，又由∠A=36°，根据等边对等角的性质，即可求得∠ABD的度数，又由AB=AC，即可求得∠ABC的度数，继而求得∠DBC的度数．

解：（1）如图：

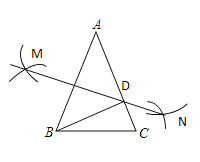
（2）解：∵AB的垂直平分线MN交AC于D，

∴AD=BD，

∵∠A=36°，

∴∠ABD=∠A=36°，

∵AB=AC，

∴∠ABC=∠C=（180°-∠A）=72°，

∴∠DBC=∠ABC-∠ABD=72°-36°=36°．