题目内容
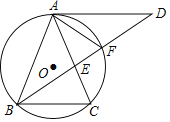
【题目】如图,己知,A(0, 4),B (t,0)分别在y轴,x轴上,连接AB,以AB为直角边分别作等腰Rt△ABD和等腰Rt△ABC.直线BC交y轴于点E. 点G(-2,3)、H(-2,1)在第二象限内.

(1)当t =-3时,求点D的坐标.
(2)若点G、H位于直线AB的异侧,确定t的取值范围.
(3)①当t取何值时,△ABE与△ACE的面积相等.
②在①的条件下,在x轴上是否存在点P,使△PCB为等腰三角形?若存在,请直接写出点P的坐标;若不存在,说明理由.
【答案】(1)D(-7,3);(2)![]() ;(3)①-2;②存在,P(6,0),P(
;(3)①-2;②存在,P(6,0),P(![]() ,0),P(-2
,0),P(-2![]() -2,0),P(2
-2,0),P(2![]() -2,0)
-2,0)
【解析】
(1)当t=-3时,过点D作DM⊥x轴于点M,证明△ABO≌△BDM,得出DM=BO和MB=OA,从而得出点D坐标.
(2)设出AB解析式y=kx+4,分别求出点G,H在线段AB上的时点B的坐标;
(3)①假设△ABE与△ACE的面积相等,利用等底同高求出t值;
②根据等腰三角形的性质,分BP=BC、CP=CB、PC=PB三种情况讨论.
(1)当t=-3时,过点D作DM⊥x轴于点M,
∵△ABD为等腰直角三角形,AB=BD,∠ABD=90°
∴∠ABO+∠DBM=180°-90°=90°
又∵DM⊥x轴于点M
∴∠DMB=90°
∴∠DBM+∠MDB=90°
∴∠MDB=∠ABO
在△ABO和△BDM中

∴△ABO≌△BDM
∴DM=BO=3,MB=OA=4
∴MO=MB+BO=4+3=7
∴D(-7,3)
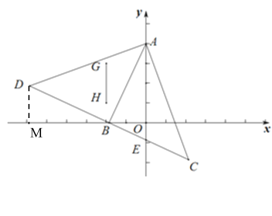
(2)∵A(0,4),B(t,0),设直线AB的解析式为y=kx+4
当点G(-2,3)在直线AB上时
3=-2k+4,![]()
此时AB的解析式![]()
当y=0时,![]() ,x=-8
,x=-8
此时B(-8,0)
当点H(-2,1)在直线AB上时
1=-2k+4,![]()
此时AB的解析式![]()
当y=0时,![]() ,x=
,x=![]()
此时B(![]() ,0)
,0)
∵点G, H位于直线AB的异侧,
∴由图像可知直线AB与线段MN相交,且点M,N不在直线AB上
∴![]()
(3)①t=-2时,△ABE与△ACE的面积相等.
如图,过点B做x轴垂线,构造直角三角形ARB和直角三角形BQC,
∵∠RAB+∠ABR=90°,∠ABR+∠BCQ=90°
∴∠ABR=∠BCQ,
在△ARB和△BQC中,
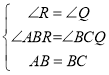 ,
,
∴△ARB≌△BQC(AAS)
∴AR=BQ,BR=QC=4,
若△ABE与△ACE的面积相等,
则BE=EC,
∴BO=CN=2,
∴B(-2,0)

②P(6,0),P(![]() ,0),P(-2
,0),P(-2![]() -2,0),P(2
-2,0),P(2![]() -2,0)
-2,0)
由②可得C(2,-2)
当BP=BC时,
BC=![]() =
=![]() ,
,
∴BP=![]()
∴P(-2![]() -2,0)或P(2
-2,0)或P(2![]() -2,0)
-2,0)
当CP=CB时,
BP=8,
∴P(6,0)
当PC=PB时,
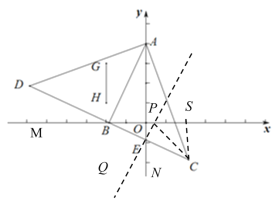
如图,过E作BC的垂线,交x轴于点P,过C作x轴垂线于点S,
设BP=m=PC,则PS=4-m,
在△PSC中,PS2+SC2=PC2,
即22+(4- m)2= m 2,
解得m=![]() ,
,
∴OP=![]() -2=
-2=![]() ,
,
∴P(![]() ,0).
,0).
综上:P(6,0),P(![]() ,0),P(-2
,0),P(-2![]() -2,0),P(2
-2,0),P(2![]() -2,0).
-2,0).

 学业测评一课一测系列答案
学业测评一课一测系列答案【题目】小林在某商店购买商品A、B共三次,只有一次购买时,商品A、B同时打折(折扣相同),其余两次均按标价购买.三次购买商品A、B的数量和费用如下表:
购买商品A的数量/个 | 购买商品B的数量/个 | 购买总费用/元 | |
第一次购物 | 6 | 5 | 1140 |
第二次购物 | 3 | 7 | 1110 |
第三次购物 | 9 | 8 | 1062 |
(1)小林以折扣价购买商品A、B是第 次购物;
(2)求出商品A、B的标价;
(3)若商品A、B的折扣相同,问商店是打几折出售这两种商品的?