题目内容
【题目】如图,∠AOB=30°,OC为∠AOB内部一条射线,点P为射线OC上一点,OP=4,点M、N分别为OA、OB边上动点,则△MNP周长的最小值为( )

A. 2 B. 4 C. ![]() D.
D. ![]()
【答案】B
【解析】
作点P关于OA的对称点P1,点P关于OB的对称点P2,连结P1P2,与OA的交点即为点M,与OB的交点即为点N,则此时M、N符合题意,求出线段P1P2的长即可.
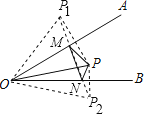
解:作点P关于OA的对称点P1,点P关于OB的对称点P2,连结P1P2,
与OA的交点即为点M,与OB的交点即为点N,此时△PMN的最小周长
∵点P关于OA的对称点为P1,关于OB的对称点为P2,连结OP1、OP2,
∴PM= P1M,OP=O P1,∠P1OA=∠POA;
∵点P关于OB的对称点为P2,
∴PN= P2N,OP=O P2,∠P2OB=∠POB,
∴OP1=OP2=OP=4,
∠P1OP2=∠P1OA+∠POA+∠POB+∠P2OB=2∠POA+2∠POB=2∠AOB=60°,
∴△OP1P2是等边三角形,
∴P1P2=OP1=4,
∴△PMN的最小周长为PM+MN+PN=P1M+MN+P2N=P1P2=4
即△PMN的周长的最小值是4.
故选:B.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目