题目内容
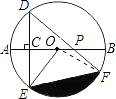
【题目】如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连结EF、EO,若DE= ![]() ,∠DPA=45°.
,∠DPA=45°.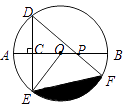
(1)求⊙O的半径;
(2)求图中阴影部分的面积.
【答案】
(1)解:∵直径AB⊥DE,∴CE= ![]() DE=
DE= ![]() .
.
∵DE平分AO,
∴CO= ![]() AO=
AO= ![]() OE.又∵∠OCE=90°,
OE.又∵∠OCE=90°,
∴sin∠CEO= ![]() =
= ![]() ,
,
∴∠CEO=30°.在Rt△COE中,OE= ![]() =
= ![]() .
.
∴⊙O的半径为2
(2)解:连接OF.
在Rt△DCP中,
∵∠DPC=45°,
∴∠D=90°﹣45°=45°.
∴∠EOF=2∠D=90°.
∴S扇形OEF= ![]() .
.
∵∠EOF=2∠D=90°,OE=OF=2,
∴SRt△OEF= ![]() ×OE×OF=2.
×OE×OF=2.
∴S阴影=S扇形OEF﹣SRt△OEF= ![]() .
.
【解析】(1)根据垂径定理求出CE的值,根据特殊角的三角函数值,求出⊙O的半径;(2)根据圆周角定理,求出∠EOF=2∠D的值,根据扇形的面积公式求出S扇形OEF的值,由△OEF的面积,得到S阴影=S扇形OEF﹣SRt△OEF的值.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目