题目内容
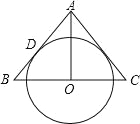
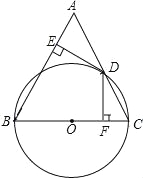
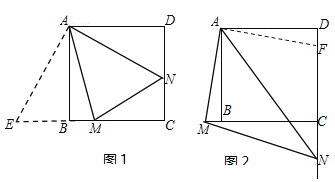
【题目】已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M,N.当∠MAN绕点A旋转到BM=DN时(如图1),易证BM+DN=MN.

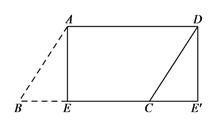
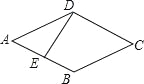
(1)当∠MAN绕点A旋转到BM≠DN时(如图2),线段BM,DN和MN之间有怎样的数量关系?写出猜想,并加以证明.
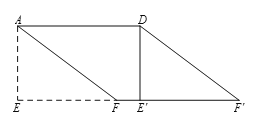
(2)当∠MAN绕点A旋转到如图3的位置时,线段BM,DN和MN之间又有怎样的数量关系?请直接写出你的猜想.
【答案】(1)BM+DN=MN成立.(2)DN-BM=MN.
【解析】试题分析:(1)、在MB的延长线上,截得BE=DN,连接AE得到△ABE≌△AND,从而得到AE=AN,然后证明△AEM≌△ANM,得到ME=MN,从而得出答案;(2)、在DC上截取DF=BM,连接AF得到△ABM≌△ADF,然后证明△MAN≌△FAN,得到所求的答案.
试题解析:(1)、BM+DN=MN成立.
如下图1,在MB的延长线上,截得BE=DN,连接AE,易证:△ABE≌△AND,∴AE=AN.
∴∠EAB=∠NMD.∴∠BAD=90°,∠NAM=45°
∴∠BAM+∠NMD=45°.∴∠EAB+∠BAM=45°.∴∠EAM=∠NAM![]() 又AM为公共边,∴△AEM≌△ANM,
又AM为公共边,∴△AEM≌△ANM,
∴ME=MN,∴ME=BE+BM=DN+BM.∴DN+BM=MN.
(2)、DN-BM=MN.
如图2,在DC上截取DF=BM,连接AF.∵AB=AD,∠ABM=∠ADF=90°,∴△ABM≌△ADF(SAS)
∴AM=AF,∠MAB=∠FAD.∴∠MAB+∠BAF=∠FAD+∠BAF=90°,即∠MAF=∠BAD=90°.
又∠MAN=45°,∴∠NAF=∠MAN=45°.∵AN=AN,∴△MAN≌△FAN.∴MN=FN,即MN=DN-DF=DN-BM;

【题目】某市语委办为了解本市八年级学生汉字书写能力情况,随机抽查了部分八年级学生,并将调查数据进行如下整理,请解答以下问题:
正确书写出的字数x(个) | 频数(人) | 频率 |
0≤x≤5 | 8 | 0.16 |
5<x≤10 | ||
10<x≤15 | 16 | 0.32 |
15<x≤20 | 8 | 0.16 |
20<x≤25 | 4 | 0.08 |
25<x≤30 | 2 | 0.04 |
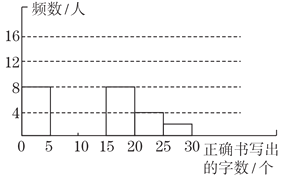
(1)把频数、频率分布表和频数分布直方图补充完整;
(2)根据统计图,可知“正确书写的字数”的中位数应处的范围是________;
(3)若正确书写的字数不超过15个为不及格,请求出不及格人数占所抽查人数的百分比;并根据调查数据估计,该市20 000名八年级学生中,有多少名学生不及格?对此,请你用一句话谈谈你的建议或感想.