题目内容
【题目】如图，点 O 为直线 AB 上一点，过点 O 作射线 OC，使∠BOC＝135°，将一个含 45°角的直角三角尺的一个顶点放在点 O 处，斜边 OM 与直线 AB 重合，另外两条直角边都在直线 AB 的下方．
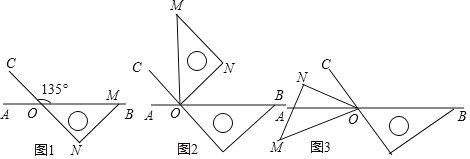
（1）将图 1 中的三角尺绕着点 O 逆时针旋转 90°，如图 2 所示，此时∠BOM＝ 度（答案直接填写在答题卡的横线上）；在图 2 中，OM 是否平分∠CON ? 请说明理由；
（2）紧接着将图 2 中的三角板绕点 O 逆时针继续旋转到图 3 的位置所示，使得 ON 在∠AOC 的内部，请探究：∠AOM 与∠CON 之间的数量关系，并说明理由；
（3）将图 1 中的三角板绕点 O 按每秒 5°的速度沿逆时针方向旋转一周，在旋转的过程中， 第 t 秒时，直线 ON 恰好平分锐角∠AOC，请你直接写出t 的值为多少．
【答案】（1）∠BOM=90°；M 是否平分∠CON，理由见解析；（2）∠AOM=∠CON，理由见解析；（3）4.5秒或40.5秒
【解析】
（1）利用旋转的性质可得∠BOM的度数，然后计算∠MOC的度数判断OM是否平分∠CON；
（2）利用∠AOM=45°-∠AON和∠NOC=45°-∠AON可判断∠AOM与∠CON之间的数量关系；
（3）ON旋转22.5度和202.5度时，ON平分∠AOC，然后利用速度公式计算t的值．
解：（1）如图2，由旋转的性质可知∠BOM=90°，
OM平分∠CON．理由如下：
∵∠BOC=135°，
∴∠MOC=135°-90°=45°，
而∠MON=45°，
∴∠MOC=∠MON；
（2）∠AOM=∠CON．
理由如下：如图3，
∵∠MON=45°，
∴∠AOM=45°-∠AON，
∵∠AOC=45°，
∴∠NOC=45°-∠AON，
∴∠AOM=∠CON；
（3）t=
×45°÷5°=4.5（秒）或t=（180°+22.5°）÷5°=40.5（秒）．
故答案为90°；4.5秒或40.5秒．
