题目内容
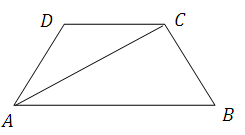
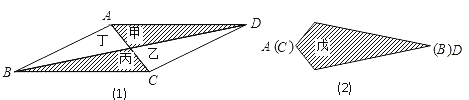
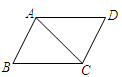
如图，在等腰梯形
中，
∥
，点
是线段上的一个动点（与
、
不重
合），
分别是
的中点．
（1）试探索四边形
的形状，并说明理由.
（2）当点运动到什么位置时，四边形是菱形？并加以证明.
（3）若（2）中的菱形是正方形，请探索线段
与线段的关系，并证明你的结论．
中，∥，点是线段上的一个动点（与、不重合），
分别是的中点．（1）试探索四边形
的形状，并说明理由.（2）当点
运动到什么位置时，四边形是菱形？并加以证明.（3）若（2）中的菱形
是正方形，请探索线段与线段的关系，并证明你的结论．（1）平行四边形，理由见解析
（2）当点是的中点时，四边形是菱形
（3）
，理由见解析
（2）当点
是的中点时，四边形是菱形（3）
，理由见解析解：（1）四边形是平行四边形.
理由：因为
分别是的中点，所以
∥
，
所以四边形是平行四边形.
（2）当点是的中点时，四边形是菱形.
证明：因为四边形是等腰梯形，所以
，
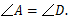
因为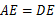
，所以△
≌△
.所以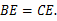
因为
分别是
的中点，所以
又由（1）知四边形是平行四边形，所以四边形是菱形.
（3）
证明：因为四边形是正方形，所以
因为分别是的中点，所以
.
因为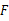
是中点，所以
是平行四边形.理由：因为
分别是的中点，所以∥，所以四边形
是平行四边形.（2）当点
是的中点时，四边形是菱形.证明：因为四边形
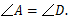
是等腰梯形，所以，因为
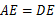，所以△≌△.所以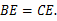因为
分别是的中点，所以又由（1）知四边形
是平行四边形，所以四边形是菱形.（3）
证明：因为四边形
是正方形，所以因为
分别是的中点，所以.因为
是中点，所以
练习册系列答案
相关题目
中，
∥
，过对角线
的中点
作
，分别交边
于点
，连接
．
是菱形；
，
，求四边形
的面积．
上时，
的长度等于（ ）．
B.
C.
D.
中，
，
，
，
，
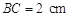，则上底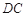
的长是_______
.