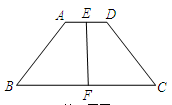
题目内容
任意四边形ABCD中,点E、F、G、H分别是AD、BC、BD、AC的中点,当四边形ABCD满足条件 时,四边形EGFH是菱形.(填一个使结论成立的条件)
AB=CD.
试题分析:E、G分别是AD,BD的中点,那么EG就是三角形ADB的中位线,同理,HF是三角形ABC的中位线,因此EG、HF同时平行且相等于AB,因此EG∥HF且EG=HF.因此四边形EHFG是平行四边形,E、H是AD,AC的中点,那么EH=
 CD,要想证明EHFG是菱形,那么就需证明EG=EH,那么就需要AB、CD满足AB=CD的条件.
CD,要想证明EHFG是菱形,那么就需证明EG=EH,那么就需要AB、CD满足AB=CD的条件.需添加条件AB=CD.
试题解析:需添加条件AB=CD.
∵点E,G分别是AD,BD的中点,
∴EG∥AB,且EG=
 AB同理HF∥AB,且HF=
AB同理HF∥AB,且HF= AB,
AB,∴EG∥HF,EG=HF.
∴四边形EGFH是平行四边形.
∵EG=
 AB,
AB,又可同理证得EH=
 CD,
CD,∵AB=CD,
∴EG=EH,
∴四边形EGFH是菱形.
故答案为:AB=CD.
考点: 1.菱形的判定;2.三角形中位线定理.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目


 △
△ 中,
中, ,
, ,将
,将 绕点
绕点 沿逆时针方向旋转
沿逆时针方向旋转 得到
得到 .
.
 的长是 ,
的长是 , 的度数是 ;
的度数是 ;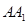 ,求证:四边形
,求证:四边形 是平行四边形.
是平行四边形. 中,
中, ∥
∥ ,点
,点 是线段
是线段 、
、 不重
不重 分别是
分别是 的中点.
的中点.
 的形状,并说明理由.
的形状,并说明理由. 与线段
与线段 中,
中, ,垂足为
,垂足为 ,
, 是
是 的平分线,
的平分线, ,垂足为
,垂足为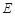 .
.
 为矩形.
为矩形. ,BD⊥AD,求BC,CD及OB的长.
,BD⊥AD,求BC,CD及OB的长.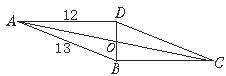
 中,
中, ∥
∥ ,∠
,∠ ∠
∠ 90°,
90°, 分别是
分别是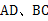 的中点,若
的中点,若 cm,
cm, cm,那么
cm,那么 ( )cm.
( )cm.