��Ŀ����
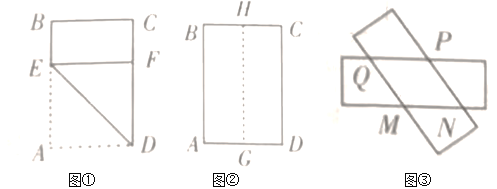
����Ŀ����һ�ž���ֽƬ![]() �У�
��![]() ��
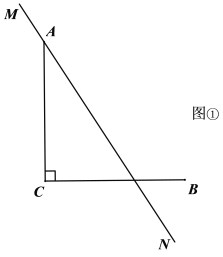
��![]() ���ֽ�����ֽƬ������ͼʾ�����۵��������������⣺
���ֽ�����ֽƬ������ͼʾ�����۵��������������⣺
��1����ͼ�٣��ۺ�Ϊ![]() ����
����![]() �Ķ�Ӧ��
�Ķ�Ӧ��![]() ��
��![]() �ϣ���֤���ı���
�ϣ���֤���ı���![]() �������Σ�
��������
��2����ͼ�ڣ�![]() ��
��![]() �ֱ�Ϊ
�ֱ�Ϊ![]() ��
��![]() ���е㣬�Ѿ���ֽƬ
���е㣬�Ѿ���ֽƬ![]() ����
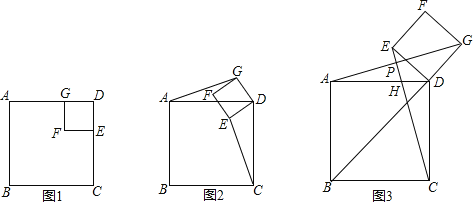
����![]() ������������ž���ֽƬ��������ֽƬ������Ϻ���ͼ�ۣ����ж��ص��ı���
������������ž���ֽƬ��������ֽƬ������Ϻ���ͼ�ۣ����ж��ص��ı���![]() ����״����֤����
����״����֤����
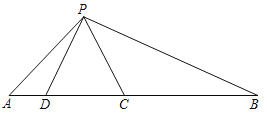
��3���ڣ�2���У��ص��ı���![]() ���ܳ��Ƿ�������ֵ����Сֵ�������ڣ���������ֵ����Сֵ���������ڣ���˵������.
���ܳ��Ƿ�������ֵ����Сֵ�������ڣ���������ֵ����Сֵ���������ڣ���˵������.
���𰸡���1������������2�����Σ�֤������������3����Сֵ12cm�����ֵ20cm.
��������
��1��������һ���ڱ���ȵľ������������ж����ɣ�
��2��������һ���ڱ���ȵ�ƽ���ı����������ж����ɣ�
��3�����ݴ��߶���̺ͽ�������ֵ�Ĺ�ϵ�ж�����.
��:��1�����ı���![]() �Ǿ��Σ�
�Ǿ��Σ�
��![]()
���۵������ʿ�֪��![]() ��
��![]() .
.
���ı���![]() �������Σ�
��������
��2���ص��ı���![]() ������
������
֤������ͼ�٣�
����������ֽƬ���Ǿ��Σ����ص��ı��εĶԱ���ƽ�У�
���ı���![]() ��ƽ���ı���.
��ƽ���ı���.

ͼ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��
�֡�![]() ��
��![]() .
.
��![]() ��
��
���ı���![]() ������
������
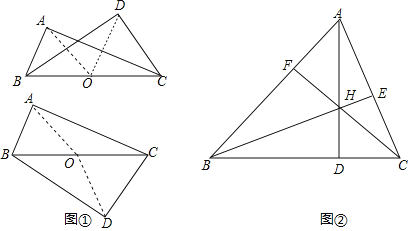
��3�����ݴ��߶���̣��ʵ���������ֽƬ���ഹֱ����ʱ����ͼ�ڣ���������ε��ܳ���СΪ![]() .
.
����![]() ����HNΪ��ֵ������HPNԽС��PN��Խ�ʵ���������ֽƬ����ͼ����ʾ����ʱ���ص����ֵ������ܳ����.
����HNΪ��ֵ������HPNԽС��PN��Խ�ʵ���������ֽƬ����ͼ����ʾ����ʱ���ص����ֵ������ܳ����.


ͼ�� ͼ��
��![]() ����
����![]() .
.
��![]() ��
��![]() ��
��
���![]() .
.
��������ε��ܳ����Ϊ![]() .
.

 ��У����ϵ�д�
��У����ϵ�д�