题目内容
【题目】如图,![]() 是正
是正![]() 内一点,
内一点,![]() ,
,![]() ,
,![]() ,将线段
,将线段![]() 以点
以点![]() 为旋转中心逆时针旋转
为旋转中心逆时针旋转![]() 得到线段
得到线段![]() ,下列结论:①
,下列结论:①![]() 可以由
可以由![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到;②点
得到;②点![]() 与
与![]() 的距离为6;③
的距离为6;③![]() ;④
;④![]() ;⑤
;⑤![]() . 其中正确的结论是______(填序号).
. 其中正确的结论是______(填序号).
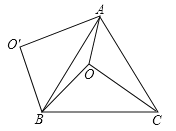
【答案】①③④.
【解析】
由正三角形和旋转性质得∠1=∠3,根据SAS得△BO′A≌△BOC,,从而得①正确;
连接OO′,由旋转性质得OB=O′B,∠OBO′=60°,根据等边三角形判定得△OBO′是等边三角形,从而得②错误;
在△AOO′中,三边长为6,8,10,这是一组勾股数,∠AOO′=90°,从而得③正确;
由①得△BO′A≌△BOC,△BO′A的面积=四边形![]() 的面积-△AOB的面积,从而得④正确;
的面积-△AOB的面积,从而得④正确;
而四边形![]() 的面积=△OBO′的面积+△O′AO的面积,从而得⑤错误.
的面积=△OBO′的面积+△O′AO的面积,从而得⑤错误.
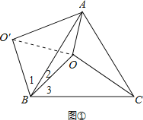
由题意可知,∠1+∠2=∠3+∠2=60°,∴∠1=∠3,
又∵OB=O′B,AB=BC,
∴△BO′A≌△BOC,又∵∠OBO′=60°,
∴△BO′A可以由△BOC绕点B逆时针旋转60°得到,
故结论①正确;
如图①,连接OO′,
∵OB=O′B,且∠OBO′=60°,
∴△OBO′是等边三角形,
∴OO′=OB=8.
故结论②错误;
∵△BO′A≌△BOC,∴O′A=10.
在△AOO′中,三边长为6,8,10,这是一组勾股数,
∴△AOO′是直角三角形,∠AOO′=90°,
∴∠AOB=∠AOO′+∠BOO′=90°+60°=150°,
故结论③正确;
![]() ,故结论④正确;
,故结论④正确;
![]() ,故结论⑤错误;
,故结论⑤错误;
故结论①③④正确.
故答案是:①③④

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目