题目内容
顺次连结等腰梯形四边中点所得到的四边形的形状是（ ）
| A．平行四边形 | B．正方形 | C．菱形 | D．矩形 |
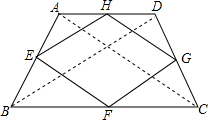
如图，已知：等腰梯形ABCD中，AD∥BC，AB=CD，E、F、G、H分别是各边的中点，
求证：四边形EFGH是菱形．
证明：连接AC、BD．
∵E、F分别是AB、BC的中点，
∴EF=
AC．
同理FG=
BD，GH=
AC，EH=
BD，
又∵四边形ABCD是等腰梯形，
∴AC=BD，
∴EF=FG=GH=HE，
∴四边形EFGH是菱形．
故选：C．
求证：四边形EFGH是菱形．
证明：连接AC、BD．
∵E、F分别是AB、BC的中点，
∴EF=
| 1 |
| 2 |
同理FG=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
又∵四边形ABCD是等腰梯形，
∴AC=BD，
∴EF=FG=GH=HE，
∴四边形EFGH是菱形．
故选：C．
练习册系列答案
黄冈创优卷系列答案
相关题目
比△DOC的周长小10cm．
