题目内容
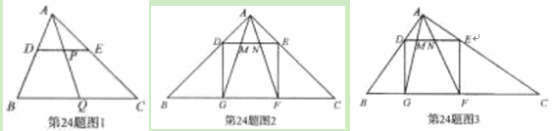
【题目】如图,在![]() △
△![]() 中,
中,![]() ,
,![]() 为斜边
为斜边![]() 上的中点,连接
上的中点,连接![]() ,以
,以![]() 为直径作⊙
为直径作⊙![]() ,分别与
,分别与![]() 、
、![]() 交于点
交于点![]() 、
、![]() .过点
.过点![]() 作
作![]() ⊥
⊥![]() ,垂足为点
,垂足为点![]() .
.
(1)求证:![]() 为⊙
为⊙![]() 的切线;
的切线;
(2)连接![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
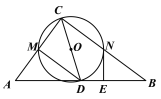
【答案】(1)见解析(2)5
【解析】
(1)欲证明NE为⊙O的切线,只要证明ON⊥NE.
(2)想办法证明四边形DMCN是矩形即可解决问题.
(1)连接ON.
∵∠ACB=90°,D为斜边的中点,∴CD=DA=DB![]() AB,∴∠BCD=∠B.
AB,∴∠BCD=∠B.
∵OC=ON,∴∠BCD=∠ONC,∴∠ONC=∠B,∴ON∥AB.
∵NE⊥AB,∴ON⊥NE,∴NE为⊙O的切线.
(2)由(1)得到:∠BCD=∠B,∴sin∠BCD=sin∠B![]() .
.
∵NE=3,∴BN=5.
连接DN.
∵CD是⊙O的直径,∴∠CND=90°,∴DN⊥BC,∴CN=BN=5,易证四边形DMCN是矩形,∴MD=CN=BN=5.


练习册系列答案
相关题目
【题目】八(2)班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队.