题目内容
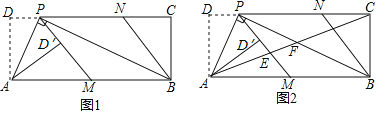
【题目】如图1,在矩形ABCD中,P为CD边上一点(DP<CP),DP=1,AD=2,∠APB=90°.将△ADP沿AP翻折得到△AD′P,PD′的延长线交边AB于点M,过点B作BN∥MP交DC于点N.

(1)求线段PC之长;
(2)求线段PN之长;
(3)如图2,连接AC,分别交PM,PB于点E,F.求线段EF之长.
【答案】(1) 4;(2) 2.5;(3)![]() .
.
【解析】
(1)证明△ADP∽△PCB,根据相似三角形对应边成比例即可得出结论;
(2)先证四边形PMBN是菱形,设菱形边长为x,由折叠的性质和勾股定理即可得出结论;
(3)在Rt△ABC中,由勾股定理求出AC.由于CP∥AB,从而可证△PCF∽△BAF,△PCE∽△MAE,得到![]() ,从而可求出EF=AF﹣AE
,从而可求出EF=AF﹣AE![]() AC
AC![]() AC,代入即可得出结论.
AC,代入即可得出结论.
(1)∵ABCD是矩形,∴AD=BC,∠D=∠C=90°,∴∠DPA+∠DAP=90°.
∵∠APB=90°,∴∠DPA+∠CPB=90°,∴∠DAP=∠CPB,∴△ADP∽△PCB,∴![]() .
.
∵AD=CB=2,∴![]() ,∴PC=4;
,∴PC=4;
(2)∵DP∥AB,∴∠DPA=∠PAM,由题意可知:∠DPA=∠APM,∴∠PAM=∠APM.
∵∠APB﹣∠PAM=∠APB﹣∠APM,即∠ABP=∠MPB,∴AM=PM,PM=MB,∴PM=MB.
∵BN∥MP,PN∥MB,∴四边形PMBN是平行四边形,∴四边形PMBN是菱形.
设菱形边长为x,则PN=PM=MB=AM=x.
由折叠可知:PD'=PD=1,AD'=AD=2,∴D'M=x-1.
在Rt△AD'M中,∵![]() ,∴
,∴![]() ,解得:x=2.5,∴PN=2.5;
,解得:x=2.5,∴PN=2.5;
(3)∵PC=4,PN=2.5,∴NC=PC-PN=1.5.在Rt△ABC中,AC=![]() .
.
∵CP∥AB,∴△PCF∽△BAF,∴![]() ,∴
,∴![]() ,∴AF=
,∴AF=![]() AC.又易证:△PCE∽△MAE,∴
AC.又易证:△PCE∽△MAE,∴![]() ,∴
,∴![]() ,∴AE=
,∴AE=![]() AC,∴EF=AF﹣AE
AC,∴EF=AF﹣AE![]() AC
AC![]() AC=
AC=![]() .
.