题目内容
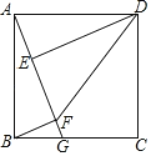
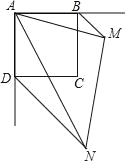
【题目】已知:如图,正方形ABCD,BM、DN分别是正方形的两个外角平分线,∠MAN=45°,将∠MAN绕着正方形的顶点A旋转,边AM、AN分别交两条角平分线于点M、N,联结MN.
(1)求证:△ABM∽△NDA;
(2)联结BD,当∠BAM的度数为多少时,四边形BMND为矩形,并加以证明.
【答案】(1)见解析;(2)22.5°.
【解析】
(1)由正方形ABCD,BM、DN分别是正方形的两个外角平分线,可证得∠ABM=∠ADN=135°,又由∠MAN=45°,可证得∠BAM=∠AND=45°-∠DAN,即可证得△ABM∽△NDA;
(2)由四边形BMND为矩形,可得BM=DN,然后由△ABM∽△NDA,根据相似三角形的对应边成比例,可证得BM2=AB2,继而求得答案.
(1)证明:∵四边形ABCD是正方形,
∴∠ABC=∠ADC=∠BAD=90°,AB=AD
∵BM、DN分别是正方形的两个外角平分线,
∴∠ABM=∠ADN=135°,
∵∠MAN=45°,
∴∠BAM=∠AND=45°﹣∠DAN,
∴△ABM∽△NDA;
(2)解:∵四边形BMND为矩形,
∴BM=DN,
∵△ABM∽△NDA,
∴![]() ,
,
∴BM2=AB2,
∴BM=AB,
∴∠BAM=∠BMA=![]() =22.5°.
=22.5°.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目