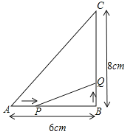
题目内容
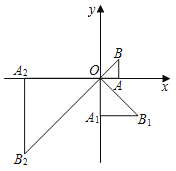
【题目】如图,四边形纸片ABCD中,AD∥BC,∠B=90°,BC=CD=6, ∠C=60°.点E是边AD上一点,连接BE,将△ABE沿BE翻折得到△HBE .
(1)当点B、D、H三点在一直线上时,求线段AE的长;
(2)当点A的对称点H正好落在DC上时,有动点P从点H出发沿线段HB向点B运动,同时动点Q从点B出发沿线段BA向点A运动,速度均为每秒1个单位长度,连接PQ交折痕BE于点M.设运动时间为t秒.
① 探究:当时间t为何值时,△PBM为等腰三角形;
② 连接AM,请直接写出BM+2AM的最小值是 .

【答案】(1)AE=6![]() -9;(2)①t=2s或
-9;(2)①t=2s或![]() s;②6
s;②6
【解析】
(1)由等边三角形的性质和直角三角形的性质可求AD=![]() DB=3,AB=
DB=3,AB=![]() AD=3
AD=3![]() ,由折叠的性质可得AB=BH=3
,由折叠的性质可得AB=BH=3![]() ,AE=EH,∠A=∠EHB=90°,由勾股定理可求解;
,AE=EH,∠A=∠EHB=90°,由勾股定理可求解;
(2)①分三种情况讨论,由等腰三角形的性质和直角三角形的性质可求解;
②过点M作MN⊥BH于N,连接AN,由三角形三边关系可得![]() BM+AM≥AN,当点A,点M,点N三点共线,且AN⊥BH时,
BM+AM≥AN,当点A,点M,点N三点共线,且AN⊥BH时,![]() BM+AM有最小值,即BM+2AM有最小值,由直角三角形的性质可求解.
BM+AM有最小值,即BM+2AM有最小值,由直角三角形的性质可求解.
解:(1)∵BC=CD=6,∠C=60°,
∴△BCD是等边三角形,
∴BD=BC=CD=6,∠C=∠DBC=∠BDC=60°,
∵AD∥BC,
∴∠DBC=∠ADB=60°,
∴∠ABD=30°,
∴AD=![]() DB=3,AB=
DB=3,AB=![]() AD=3
AD=3![]() ,
,
当点B、D、H三点在一直线上时,如图,

∵将△ABE沿BE翻折得到△HBE,
∴AB=BH=3![]() ,AE=EH,∠A=∠EHB=90°,
,AE=EH,∠A=∠EHB=90°,
∴DH=6-3![]() ,
,
∵DE2=EH2+DH2,
∴(3-AE)2=AE2+(6-3![]() )2,
)2,
∴AE=6![]() -9
-9
(2)①∵将△ABE沿BE翻折得到△HBE,当点A的对称点H正好落在DC上,且∠ADB=∠CDB=60°,
∴点E与点D重合,AB=BH=2![]() ,∠ABE=∠HBE=30°,
,∠ABE=∠HBE=30°,
如图,若BM=PM时,则∠MPB=∠MBP=30°,

∴∠QMB=60°,
∴∠BQP=90°,
又∵∠QPB=30°,
∴BP=2QB,
∴2![]() -t=t,
-t=t,
∴t=![]() ,
,
如图,若BM=BP时,则∠BPM=∠BMP=75°,
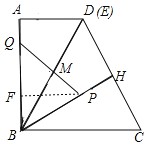
∴∠BQM=∠BMP-∠ABD=45°,
过点P作PF⊥AB于F,
∴△PFQ是等腰直角三角形,
∴PF=FQ,
∵∠PBF=60°,PF⊥AB,
∴∠BPF=30°,
∴BF=![]() BP=
BP=![]() (2
(2![]() -t),PF=
-t),PF=![]() BF=
BF=![]() (2
(2![]() -t)=QF,
-t)=QF,
∵BQ=BF+QF,
∴t=![]() (2
(2![]() -t)+
-t)+![]() (2
(2![]() -t),
-t),
∴t=2,
当BP=PM时,不合题意舍去,
综上所述:当t=2s或![]() s时,△PBM为等腰三角形;
s时,△PBM为等腰三角形;
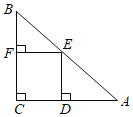
②如图,过点M作MN⊥BH于N,连接AN,

∵∠MBN=30°,MN⊥BH,
∴MN=![]() BM,
BM,
∴BM+2AM=2(![]() BM+AM),
BM+AM),
∵MN+AM≥AN,
∴![]() BM+AM≥AN,
BM+AM≥AN,
∴当点A,点M,点N三点共线,且AN⊥BH时,![]() BM+AM有最小值,即BM+2AM有最小值,
BM+AM有最小值,即BM+2AM有最小值,
此时,AN⊥BH,∠ABN=60°,
∴BN=![]() AB=
AB=![]() ,AN=
,AN=![]() BN=3,
BN=3,
∴BM+2AM最小值为6,
故答案为:6.

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案【题目】某超市计划购进甲、乙两种商品,两种商品的进价、售价如下表:
商品 | 甲 | 乙 |
进价(元/件) |
|
|
售价(元/件) | 200 | 100 |
若用360元购进甲种商品的件数与用180元购进乙种商品的件数相同.
(1)求甲、乙两种商品的进价是多少元?
(2)若超市销售甲、乙两种商品共50件,其中销售甲种商品为![]() 件(
件(![]() ),设销售完50件甲、乙两种商品的总利润为
),设销售完50件甲、乙两种商品的总利润为![]() 元,求
元,求![]() 与
与![]() 之间的函数关系式,并求出
之间的函数关系式,并求出![]() 的最小值.
的最小值.