题目内容
【题目】如图,在平面直角坐标系xOy中,有一个等腰直角三角形AOB,∠OAB=90°,直角边AO在x轴上,且AO=1.将Rt△AOB绕原点O顺时针旋90°转得到等腰直角三角形A1OB1,且A1O=2AO,再将Rt△A1OB1绕原点O顺时针旋转90°得到等腰直角三角形A2OB2,且A2O=2A1O,…,依此规律,得到等腰直角三角形A2020OB2020,则点B2020的坐标为_____.
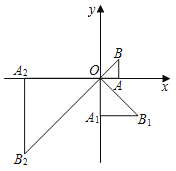
【答案】(22020,22020).
【解析】
根据题意得出B点坐标变化规律,进而得出点B2020的坐标位置,进而得出答案.
∵△AOB是等腰直角三角形,OA=1,
∴AB=OA=1,
∴B(1,1),
将Rt△AOB绕原点O顺时针旋转90°得到等腰直角三角形A1OB1,且A1O=2AO,
再将Rt△A1OB1绕原点O顺时针旋转90°得到等腰三角形A2OB2,且A2O=2A1O…,依此规律,
∴每4次循环一周,B1(2,﹣2),B2(﹣4,﹣4),B3(﹣8,8),B4(16,16),
∵2020÷4=505,
∴点B2020与B同在一个象限内,
∵﹣4=﹣22,8=23,16=24,
∴点B2020(22020,22020).
故答案为(22020,22020).

练习册系列答案
相关题目